题目内容
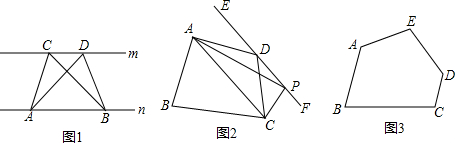
如图，两点A、B在直线MN外的同侧，A到MN的距离AC=8，B到MN的距离BD=5，CD=4，P在直线MN上运动，则|PA-PB|的最大值等于分析：延长AB交MN于点P′，此时P′A-P′B=AB，由三角形三边关系可知AB＞|PA-PB|，故当点P运动到P′点时
|PA-PB|最大，作BE⊥AM，由勾股定理即可求出AB的长．
|PA-PB|最大，作BE⊥AM，由勾股定理即可求出AB的长．
解答：
解：延长AB交MN于点P′，
∵P′A-P′B=AB，AB＞|PA-PB|，
∴当点P运动到P′点时，|PA-PB|最大，
∵BD=5，CD=4，AC=8，
过点B作BE⊥AC，则BE=CD=4，AE=AC-BD=8-5=3，
∴AB=
=
=5．
∴|PA-PB|=5为最大．
故答案为：5．
解：延长AB交MN于点P′，∵P′A-P′B=AB，AB＞|PA-PB|，
∴当点P运动到P′点时，|PA-PB|最大，
∵BD=5，CD=4，AC=8，
过点B作BE⊥AC，则BE=CD=4，AE=AC-BD=8-5=3，
∴AB=
| AE2+BE2 |
| 32+42 |
∴|PA-PB|=5为最大．
故答案为：5．
点评：本题考查的是最短线路问题及勾股定理，熟知两点之间线段最短及三角形的三边关系是解答此类问题的关键．
练习册系列答案
相关题目
（2013•龙湾区一模）如图，热气球从山顶A竖直上升至点B需25秒，点D在地面上，DC⊥AB，垂足为C，从地面上点D分别仰视A，B两点，测得∠ADC=20°，∠BDC=60°，若CD=130米．求该热气球从山顶A竖直上升至点B的平均速度．（结果精确到0.1米/秒）
如图，热气球从山顶A竖直上升至点B需25秒，点D在地面上，DC⊥AB，垂足为C，从地面上点D分别仰视A，B两点，测得∠ADC=20°，∠BDC=60°，若CD=130米．求该热气球从山顶A竖直上升至点B的平均速度．（结果精确到0.1米/秒）
