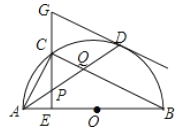
题目内容
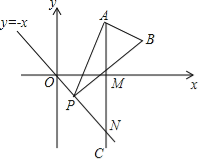
【题目】如图，在
中，
是直径，点
是上一点，点
是
的中点，
于点
，过点的切线交
的延长线于点
，连接
，分别交
于点
，连接
，交于下列结论：
①
；
②
；
③点
是
的外心，
④
其中正确结论是_________________（只需填写序号）．
【答案】②③
【解析】
①利用圆周角定理的推论和弧之间的关系即可判断；
②连接OD，利用等腰三角形的性质得出
，再根据
即可得出
，由此可判断②的正误；
③首先利用垂径定理证明
，则有
，进而利用圆周角定理的推论和等量代换得出
，则
，P点为
斜边AQ中点，则可判断③的正误；
④利用同位角
与
是否相等即可判断两直线是否平行．
①∵点
是
的中点，
，
．
∵
与
不一定相等，
∴
与
不一定相等，故①错误；
②如图，
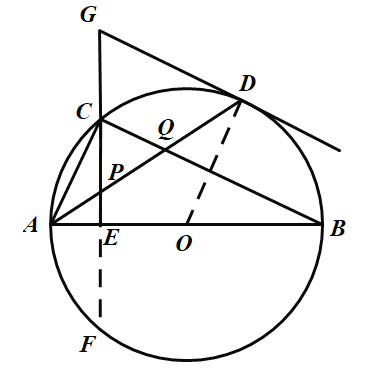
连接OD，则
，
．
，
，
，故②正确；
③
于点
，
∴F为CE中点，
∴
．
∵点是的中点，
，
，
，
．
∵AB为圆的直径，
，
，
，
，
，
∴P点为斜边AQ中点，
∴点
是
的外心，故③正确；
④
，
，
又
与
不一定相等，
∴与不一定相等，
∴BC与GD不一定平行；
所以正确的有：②③，
故答案为：②③．
练习册系列答案
相关题目
