题目内容
如图，直线y=-2x+7与两条坐标轴分别交于点P、Q，在线段PQ上有一点A，过A作两条坐标轴的垂线，垂足分别为B、C，若矩形ABOC的面积等于5，则点A的坐标为（1，5）或（
，2）
| 5 |
| 2 |
（1，5）或（
，2）
．| 5 |
| 2 |
分析：先设A点坐标为（x，-2x+7），再由矩形的面积公式求出x的值即可．
解答：解：设A点坐标为（x，-2x+7），则OC=-2x+7，OB=x，
∵矩形ABOC的面积等于5，
∴x（-2x+7）=5，解得x=1或x=
，
当x=1时，-2x+7=-2+7=5；当x=
时，-2x+7=（-2）×
+7=2，
∴点A的坐标为 （1，5）或（
，2）．
故答案为：（1，5）或（
，2）．
∵矩形ABOC的面积等于5，
∴x（-2x+7）=5，解得x=1或x=
| 5 |
| 2 |
当x=1时，-2x+7=-2+7=5；当x=
| 5 |
| 2 |
| 5 |
| 2 |
∴点A的坐标为 （1，5）或（
| 5 |
| 2 |
故答案为：（1，5）或（
| 5 |
| 2 |
点评：本题考查的是一次函数图象上点的坐标特点及矩形的面积公式，熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
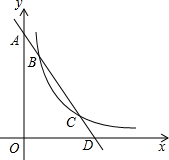如图，直线y=-2x+b与y轴交于点A，与x轴交于点D，与双曲线
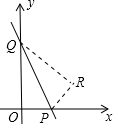如图，直线y=-2x+6与x轴、y轴分别交于P、Q两点，把△POQ沿PQ翻折，点O落在R处，则点R的坐标是
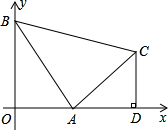腰直角△ABC，∠BAC=90°，过C作CD⊥x轴，垂足为D．
轴分别交于点C、D．直线EB交x轴于点F．
如图，直线y=-2x+8与两坐标轴分别交于P，Q两点，在线段PQ上有一点A，过点A分别作两坐标轴的垂线，垂足分别为B、C．