题目内容
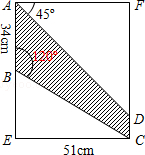 丁丁想在一个矩形材料中剪出如图阴影所示的梯形,作为要制作的风筝的一个翅膀.请你根据图中的数据帮丁丁计算:
丁丁想在一个矩形材料中剪出如图阴影所示的梯形,作为要制作的风筝的一个翅膀.请你根据图中的数据帮丁丁计算:(1)BE的长度;
(2)阴影部分的面积(精确到个位).
考点:解直角三角形的应用
专题:
分析:(1)在直角△BCE中,利用三角函数即可求得BE的长度;
(2)首先证明△ACF是等腰三角形,求得FC的长度,进而得到CD的长,然后利用梯形的面积公式即可求解.
(2)首先证明△ACF是等腰三角形,求得FC的长度,进而得到CD的长,然后利用梯形的面积公式即可求解.
解答:解:(1)在直角△BCE中,∠EBC=180°-120°=60°,
则tan∠EBC=
,
∴BE=
=
=
=17
(cm);
(2)在直角△ACF中,∠ADF=90°-∠FAD=90°-45°=45°.
∴∠FAD=∠ADF,
∴FD=AF=EC=51cm.
又∵FC=AE=AB+BE=34+17
(cm).
∴CD=34+17
-51=17
-17(cm).
则S阴影=
(AB+CD)×EC=
(34+17
-17)×51=
(17
+17)≈1184(cm2).
则tan∠EBC=
| EC |
| BE |

∴BE=
| EC |
| tan∠EBC |
| 51 |
| tan60° |
| 51 | ||
|
| 3 |
(2)在直角△ACF中,∠ADF=90°-∠FAD=90°-45°=45°.
∴∠FAD=∠ADF,
∴FD=AF=EC=51cm.
又∵FC=AE=AB+BE=34+17
| 3 |
∴CD=34+17
| 3 |
| 3 |
则S阴影=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 51 |
| 2 |
| 3 |
点评:本题考查了三角函数以及等腰三角形的判定定理,正确求得CD的长度是关键.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
下列方程组中,二元一次方程组是( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
 如图,在圆心角为直角的扇形OAB中,分别以OA、OB为直径作两个半圆,向直角扇形OAB内随机取一点,则该点刚好来自阴影部分的概率是( )
如图,在圆心角为直角的扇形OAB中,分别以OA、OB为直径作两个半圆,向直角扇形OAB内随机取一点,则该点刚好来自阴影部分的概率是( )A、1-
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,△ACF内接于⊙O,AB是⊙O直径,弦CD⊥AB于E,若CD=BE=8,则sin∠AFC的值为( )
如图,△ACF内接于⊙O,AB是⊙O直径,弦CD⊥AB于E,若CD=BE=8,则sin∠AFC的值为( )A、
| ||||
B、
| ||||
C、
| ||||
| D、以上都不对 |
 已知:正方形ABCD中,E,F分别是边CD,DA上的点,且CE=DF,AE与BF交于点M.
已知:正方形ABCD中,E,F分别是边CD,DA上的点,且CE=DF,AE与BF交于点M.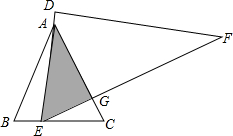 如图,等边△ABC中,AB=6,将一直角三角板DEF的60°角的顶点E置于边BC上移动(不与B、C重合),移动过程中,始终满足直角边DE经过点A,斜边EF交AC于点G.
如图,等边△ABC中,AB=6,将一直角三角板DEF的60°角的顶点E置于边BC上移动(不与B、C重合),移动过程中,始终满足直角边DE经过点A,斜边EF交AC于点G. 如图,AB∥CD,∠A=70°,则∠COE=
如图,AB∥CD,∠A=70°,则∠COE=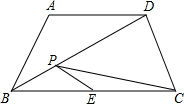 如图所示,在等腰梯形ABCD中,AD∥BC,∠A=120°,AB=AD=2,点E是BC的中点,点P是对角线BD上的动点,则PE+PC的最小值是( )
如图所示,在等腰梯形ABCD中,AD∥BC,∠A=120°,AB=AD=2,点E是BC的中点,点P是对角线BD上的动点,则PE+PC的最小值是( )