Question

如图，AB、CD是两条相互垂直的公路，设计时想在拐弯处用一段圆弧形湾道把它们连接起来（圆弧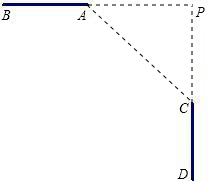在A、C两点处分别与道路相切），测得AC=60米，∠ACP=45度．
（1）在图中画出圆弧形弯道的示意图；
（2）求弯道部分的长．（结果保留四个有效数字）．

Answer 1

分析：（1）利用切线定义作圆，使圆与AB，CD相切，弧AC就是所要画的弯道；
（2）弯道是一段弧长，那么利用弧长公式即可求出．

解答：解：（1）分别从点A，C处作垂线，两垂线相交于点O，以点O为圆心，OA为半径作圆，弧

AC

就是所求的弯道；（3分）


（2）由题意及作图过程可得：∠AOC=90°
∴0A=OC=

2

2

•AC=30

2

m
∴弧AC的长=

90

180

π•OA=15

2

•π≈66.64（米）（或66.60米）
即：弯道部分的长约为66.64米（或66.60米）．（6分）

点评：本题主要考查了学生的画题能力，及利用弧长公式解决实际问题的能力．