Question

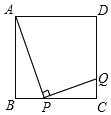
【题目】如图，在正方形ABCD中，AB=4，点P、Q分别在直线CB与射线DC上（点P不与点C、点B重合），且保持∠APQ=90°，CQ=1，则线段BP的长为_____．

Answer 1

【答案】2或2﹣2或2+2

【解析】

设BP＝x，分三种情况讨论：①当P在线段BC上时，如图1，②当P在CB的延长线上时，如图2，③当P在BC的延长线上时，如图3，证明：△ABP∽△PCQ，列比例式可得对应x的值．

设BP＝x，分三种情况讨论：

①当P在线段BC上时，如图1．

∵四边形ABCD是正方形，∴∠B＝∠C＝90°，∴∠BAP+∠APB＝90°．

∵∠APQ＝90°，∴∠APB+∠CPQ＝90°，∴∠BAP＝∠CPQ，∴△ABP∽△PCQ，∴，∴，∴x1＝x2＝2，∴BP＝2；

②当P在CB的延长线上时，如图2，同瑆得：△ABP∽△PCQ，∴，∴，x2+4x﹣4＝0，x＝﹣2+2或﹣2﹣2（舍）；

③当P在BC的延长线上时，如图3，同瑆得：△ABP∽△PCQ，∴，∴，x2﹣4x﹣4＝0，x＝2+2或2﹣2（舍）．

综上所述：线段BP的长为2或22或22．

故答案为：2或22或22．