题目内容

抛物线y=ax²+bx+c，a＞0，c＜0，2a+3b+6c=0．
（1）求证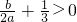： $数学公式$ ；
（2）抛物线经过点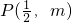 $数学公式$ ，Q（1，n）．
①判断mn的符号；
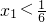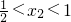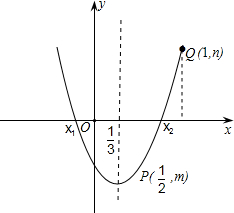②若抛物线与x轴的两个交点分别为点A（x₁，0），点B（x₂，0）（点A在点B左侧），请说明 $数学公式$ ， $数学公式$ ．

（1）证明：∵2a+3b+6c=0，
∴ $\text{[math]}$ ．
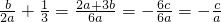∵a＞0，c＜0，
∴ $\text{[math]}$ ， $\text{[math]}$ ．
∴ $\text{[math]}$ ．

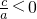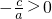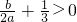（2）解：∵抛物线经过点P 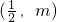$\text{[math]}$ ，点Q（1，n），
∴ $\text{[math]}$
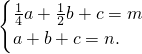
①∵2a+3b+6c=0，a＞0，c＜0，
∴ $\text{[math]}$ ， $\text{[math]}$ ．
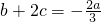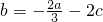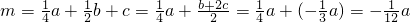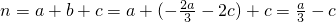∴ $\text{[math]}$ ＜0. $\text{[math]}$ ＞0．
∴mn＜0．
②由a＞0知抛物线y=ax²+bx+c开口向上．
∵m＜0，n＞0，
∴点P 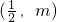$\text{[math]}$ 和点Q（1，n）分别位于x轴下方和x轴上方．
∵点A，B的坐标分别为A（x₁，0），B（x₂，0）（点A在点B左侧），
∴由抛物线y=ax²+bx+c的示意图可知，
对称轴右侧的点B的横坐标x₂满足 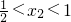$\text{[math]}$ ．（如图所示）
∵抛物线的对称轴为直线 $\text{[math]}$ ，
由抛物线的对称性可 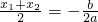$\text{[math]}$ ，由（1）知 $\text{[math]}$ ，
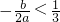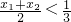∴ $\text{[math]}$ ．即x₁+x₂＜ $\text{[math]}$ ，
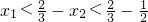∴ $\text{[math]}$ = $\text{[math]}$ ，即 $\text{[math]}$ ．
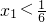分析：（1）因为2a+3b+6c=0，所以2a+3b=-6c，再把 $\text{[math]}$ + $\text{[math]}$ 通分，利用条件a＞0，c＜0，问题可得证；
（2）①把P，Q两点的坐标分别代入，可得到关于m，n的关系式，再有条件a＞0，c＜0，2a+3b+6c=0，可判断mn的符号；
②因为a＞0，知抛物线y=ax²+bx+c开口向上．又因为抛物线与x轴的两个交点分别为点A（x₁，0），点B（x₂，0）（点A在点B左侧），所以把抛物线y=ax²+bx+c的示意图画出，利用抛物线的对称性可证得问题的正确性．
点评：本题主要考二次函数系数和与x轴的交点问题，把抛物线与坐标轴的交点问题转化为与二元一次方程有关的问题是解答此题的关键，重点是从图象中找出重要信息．