Question

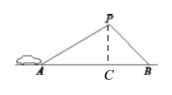
【题目】某条道路上通行车辆限速为60千米/时，在离道路50米处建有一个监测点P，道路AB段为检测区(如图)．在△ABP中，已知∠PAB＝32°，∠PBA＝45°，那么车辆通过AB段的时间在多少秒以内时，可认定为超速？(精确到0.1秒．参考数据：sin32°≈0.53，cos32°≈0.85，tan32°≈0.62)

Answer 1

【答案】7.8秒

【解析】

如下图，过点P作PC⊥AB于点C，由题意可得PC=50米，这样在Rt△PAC和Rt△PBC中分别由已知条件解得AC和BC的长，即可由已知条件求得所求的时间了.

如下图，过点P作PC⊥AB于点C，

∴∠PCA=∠PCB=90°，

∵在Rt△APC中，tan∠PAC＝，

∴AC＝≈80.65(米)．

同理，在Rt△PBC中可得：BC＝＝50(米)．

∴AB＝AC＋BC≈130.65(米)．

∵60千米/时＝米/秒，则130.65÷≈7.8(秒)．

∴当车辆通过AB段的时间在7.8秒内时，可认定为超速．