题目内容
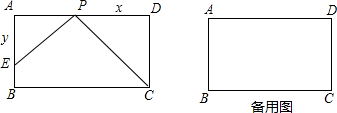
已知矩形ABCD中,AD=nAB,E为AB的中点,BF⊥CE于点F,过点F作DF的垂线交直线BC于G.
(1)如图1,当n=1 时,求证:△BFG∽△CFD ;
 |
![]()
(2)如图2,当n=2 时,求证:CG=7BG .
 |
![]()
解:(1)证明: ∵∠ABC=90°
∴∠BEC+∠BCE=90°
 又∵BF⊥EC
又∵BF⊥EC
∴∠FBC+∠BCE=90°
∴∠BEC=∠FBC
又∵AB∥DC
∴∠BEC=∠ECD
∴∠FBC=∠ECD ① --------2分
又∵BF⊥EC,FG⊥FD
∴∠BFG+∠GFC=∠GFC+∠CFD=90°
 ∴∠BFG=∠CFD ② --------4分
∴∠BFG=∠CFD ② --------4分
由①、②得:△BFG∽△CFD --------5分
(2)证明:∵AD=2AB,AB=2BE
∴AD=BC=4BE 即![]()
∵∠ECB公共,∠CFB=∠CBE=90°
 ∴△CFB∽△CBE --------7分
∴△CFB∽△CBE --------7分
∴![]()
由第(1)问得△BFG∽△CFD
∴![]() ------9分
------9分
又∵AD=BC=2AB=2CD
∴![]()
∴![]() --------10分
--------10分

练习册系列答案
相关题目
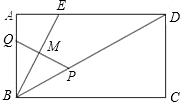 ,点Q从点B以每秒1个单位沿BA方向向点A运动,设运动时间为t秒,△BPQ的面积为S.
,点Q从点B以每秒1个单位沿BA方向向点A运动,设运动时间为t秒,△BPQ的面积为S. 如图,已知矩形ABCD中,BC=6,AB=8,延长AD到点E,使AE=15,连接BE交AC于点P.
如图,已知矩形ABCD中,BC=6,AB=8,延长AD到点E,使AE=15,连接BE交AC于点P. 如图:已知矩形ABCD中,CE∥DF.
如图:已知矩形ABCD中,CE∥DF.