题目内容
已知AB=A′B′，∠A=∠A′，∠B=∠B′，则△ABC≌△A′B′C′的根据是
- A.SAS
- B.SSA
- C.ASA
- D.都行
C
分析：本题画图后就一目了然了，观察已知条件在图形上的位置，是两角与其夹边对应相等，符合SAS，于是答案可得．
解答：
解：如图，∵AB=A′B′，∠A=∠A′，∠B=∠B′
∴AB是∠A与∠B的夹边，A′B′是∠A′与∠B′的夹边
∴△ABC≌△A′B′C′的根据是ASA．
故选C．
点评：本题重点考查了三角形全等的判定定理，普通两个三角形全等共有四个定理，即AAS，ASA，SAS，SSS，直角三角形可用HL．根据位置结合判定方法进行判定．
分析：本题画图后就一目了然了，观察已知条件在图形上的位置，是两角与其夹边对应相等，符合SAS，于是答案可得．
解答：
解：如图，∵AB=A′B′，∠A=∠A′，∠B=∠B′∴AB是∠A与∠B的夹边，A′B′是∠A′与∠B′的夹边
∴△ABC≌△A′B′C′的根据是ASA．
故选C．
点评：本题重点考查了三角形全等的判定定理，普通两个三角形全等共有四个定理，即AAS，ASA，SAS，SSS，直角三角形可用HL．根据位置结合判定方法进行判定．
练习册系列答案
相关题目
10、如图，已知AB是⊙O的直径，C是⊙O外一点，CA、CB交⊙O分别于D、E点，且AB=1，则cos∠C=（ ）
如图：折叠长方形ABCD（四个角都是直角，对边相等）的一边AD，点D落在BC边的F处，已知AB=8cm，BC=10cm，则EC=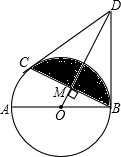
如图，已知AB为⊙O的直径，BD为⊙O的切线，过点B的弦BC⊥OD交⊙O于点C，垂足为M．