题目内容
(1)观察发现
如图①,⊙O的半径为1,点P为⊙O外一点 ,PO=2,在⊙O上找一点M,使得PM最长。
做法如下:作射线PO交⊙O于点M,则点M就是所求的点,此时PM=________。
请说明PM最长的理由。
(2)实践运用
如图②,在等边三角形 ABC中,AB=2,以AB为斜边作直角三角形AMB,使CM最长.
做法如下:以AB为直径画⊙O,作射线CO交⊙O右侧于点M,则△AMB即为所求。
 请按上述方法用三角板和圆规画出图形,并求出CM的长度。
请按上述方法用三角板和圆规画出图形,并求出CM的长度。
图① 图② 图③
(3)拓展延伸
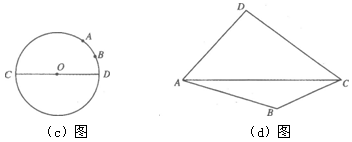
如图③,在周长为m的任意形状的△ABC中,分别以AB、AC为斜边作直角三角形AMB,直角三角形ANC,使得线段MN最长,用尺规画出图形, 此时MN=_______。(保留作图痕迹)。 ![]()
 (1)PM= 3 ,(1分)
(1)PM= 3 ,(1分)
在圆上任取一点M![]() ,
,
PM=PO+OM![]() ≥PM
≥PM![]() (2分)
(2分)
(2)如图 (1分) MN=![]() ,)
,)
(3)如图![]() (尺规画垂直平分线)(2分) MN=0.5m (1分)
(尺规画垂直平分线)(2分) MN=0.5m (1分)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 同侧,在直线
同侧,在直线 ,连接
,连接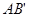 ,与直线
,与直线
 同侧,在直线
同侧,在直线 ,连接
,连接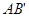 ,与直线
,与直线

 同侧,在直线
同侧,在直线 ,连接
,连接 ,与直线
,与直线

