题目内容
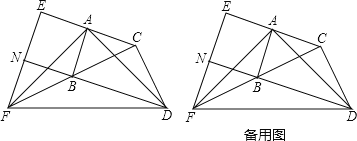
【题目】已知射线![]() 在
在![]() 的内部,射线
的内部,射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() .
.
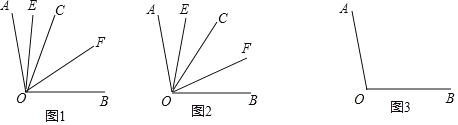
(1)如图1,若![]() ,则
,则![]() __________度;
__________度;
(2)若![]() ,
,
①如图2,若射线![]() 在
在![]() 的内部绕点
的内部绕点![]() 旋转,求
旋转,求![]() 的度数;
的度数;
②若射线![]() 在
在![]() 的外部绕点
的外部绕点![]() 旋转(旋转中
旋转(旋转中![]() 、
、![]() 均是指小于180°的角),其余条件不变,请借助图3探究
均是指小于180°的角),其余条件不变,请借助图3探究![]() 的大小,直接写出
的大小,直接写出![]() 的度数.
的度数.
【答案】(1)60;(2)①∠EOF=![]() α;②当射线OE,OF只有1条在∠AOB外部时,∠EOF=
α;②当射线OE,OF只有1条在∠AOB外部时,∠EOF=![]() α;当射线OE,OF都在∠AOB外部时,∠EOF=180°-
α;当射线OE,OF都在∠AOB外部时,∠EOF=180°-![]() α.
α.
【解析】
(1)先求出∠BOC度数,根据角平分线定义求出∠EOC和∠FOC的度数,求和即可得出答案;
(2)①根据角平分线定义得出∠COE=![]() ∠AOC,∠COF=
∠AOC,∠COF=![]() ∠BOC,求出∠EOF=∠EOC+∠FOC=
∠BOC,求出∠EOF=∠EOC+∠FOC=![]() ∠AOB,代入求出即可;
∠AOB,代入求出即可;
②分两种情况:当射线OE,OF只有1条在∠AOB外部时,根据角平分线定义得出∠COE=![]() ∠AOC,∠COF=
∠AOC,∠COF=![]() ∠BOC,求出∠EOF=∠FOC-∠COE=
∠BOC,求出∠EOF=∠FOC-∠COE=![]() ∠AOB;当射线OE,OF都在∠AOB外部时,根据角平分线定义得出∠EOF=
∠AOB;当射线OE,OF都在∠AOB外部时,根据角平分线定义得出∠EOF=![]() ∠AOC,∠COF=
∠AOC,∠COF=![]() ∠BOC,求出∠EOF=∠EOC+∠COF=
∠BOC,求出∠EOF=∠EOC+∠COF=![]() (360°-∠AOB),代入求出即可.
(360°-∠AOB),代入求出即可.
解:(1)∵∠AOB=120°,∠AOC=32°,
∴∠BOC=∠AOB-∠AOC=88°,
∵OE,OF分别是∠AOC和∠COB的角平分线,
∴∠EOC=![]() ∠AOC=16°,∠FOC=
∠AOC=16°,∠FOC=![]() ∠BOC=44°,
∠BOC=44°,
∴∠EOF=∠EOC+∠FOC=16°+44°=60°.
故答案为:60;
(2)①∵OE,OF分别是∠AOC和∠COB的角平分线,
∴∠EOC=![]() ∠AOC,∠FOC=
∠AOC,∠FOC=![]() ∠BOC,
∠BOC,
∴∠EOF=∠EOC+∠FOC=![]() ∠AOB=
∠AOB=![]() α;
α;
②分以下两种情况:
当射线OE,OF只有1条在∠AOB外部时,如图3①,
∠EOF=∠FOC-∠COE=![]() ∠BOC-
∠BOC-![]() ∠AOC=
∠AOC=![]() (∠BOC-∠AOC)=
(∠BOC-∠AOC)=![]() ∠AOB=
∠AOB=![]() α.
α.
当射线OE,OF都在∠AOB外部时,如图3②,
∠EOF=∠EOC+∠COF=![]() ∠AOC+
∠AOC+![]() ∠BOC=
∠BOC=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() (360°-∠AOB)=180°-
(360°-∠AOB)=180°-![]() α.
α.
综上所述,当射线OE,OF只有1条在∠AOB外面时,∠EOF=![]() α;当射线OE,OF都在∠AOB外部时,∠EOF=180°-
α;当射线OE,OF都在∠AOB外部时,∠EOF=180°-![]() α.
α.

【题目】如图所示的是丽水市统计局公布的2010~2013年全社会用电量的折线统计图.

(1)根据统计图填写统计表:
2010~2013年丽水市全社会用电量统计表
年份 | 2010 | 2011 | 2012 | 2013 |
全社会用电量 (单位:亿KW·h) | 13.33 |
(2)根据丽水市2010年至2013年全社会用电量统计数据,求2011~2013年全社会用电量的年平均增长率(保留到0.01).