题目内容
用“描点法”画二次函数y=ax2+bx+c的图象时,列了如下表格:
| x | 0 | 1 | 2 | 3 | ||
| y | 3 | 0 | -1 | 0 |
<
分析:先根据图表数据可知二次函数图象的对称轴为直线x=2,并且在对称轴的左侧,y随x的增大而减小;在对称轴的右侧,y随x的增大而增大,得出a>0,再根据点P与点Q距离对称轴的远近,判断其函数值的大小,从而得解.
解答:由题意,可得二次函数图象的对称轴为直线x=2,
并且在对称轴的左侧,y随x的增大而减小;在对称轴的右侧,y随x的增大而增大,
∴a>0,
∵点P与点Q中,当P距离对称轴较近,
∴a<b.
故答案为<.
点评:本题考查了二次函数图象的性质,根据表中数据得到函数的对称轴为直线x=2及a>0是解题的关键.
分析:先根据图表数据可知二次函数图象的对称轴为直线x=2,并且在对称轴的左侧,y随x的增大而减小;在对称轴的右侧,y随x的增大而增大,得出a>0,再根据点P与点Q距离对称轴的远近,判断其函数值的大小,从而得解.
解答:由题意,可得二次函数图象的对称轴为直线x=2,
并且在对称轴的左侧,y随x的增大而减小;在对称轴的右侧,y随x的增大而增大,
∴a>0,
∵点P与点Q中,当P距离对称轴较近,
∴a<b.
故答案为<.
点评:本题考查了二次函数图象的性质,根据表中数据得到函数的对称轴为直线x=2及a>0是解题的关键.

练习册系列答案
相关题目

 的图象时,列了如下表格:
的图象时,列了如下表格:






 ,当
,当 时,函数值
时,函数值 。
。

 的图象时,列了如下表格:
的图象时,列了如下表格: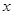


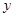



 ,当
,当 时,函数值
时,函数值 。
。