题目内容
（2013•河北）如图1，M是铁丝AD的中点，将该铁丝首尾相接折成△ABC，且∠B=30°，∠C=100°，如图2．则下列说法正确的是（ ）分析：根据钝角三角形中钝角所对的边最长可得AB＞AC，取BC的中点E，求出AB+BE＞AC+CE，再根据三角形的任意两边之和大于第三边得到AB＜
AD，从而判定AD的中点M在BE上．
| 1 |
| 2 |
解答：
解：∵∠C=100°，
∴AB＞AC，
如图，取BC的中点E，则BE=CE，
∴AB+BE＞AC+CE，
由三角形三边关系，AC+BC＞AB，
∴AB＜
AD，
∴AD的中点M在BE上，
即点M在BC上，且距点B较近，距点C较远．
故选C．
解：∵∠C=100°，∴AB＞AC，
如图，取BC的中点E，则BE=CE，
∴AB+BE＞AC+CE，
由三角形三边关系，AC+BC＞AB，
∴AB＜
| 1 |
| 2 |
∴AD的中点M在BE上，
即点M在BC上，且距点B较近，距点C较远．
故选C．
点评：本题考查了三角形的三边关系，作辅助线把△ABC的周长分成两个部分是解题的关键，本题需要注意判断AB的长度小于AD的一半，这也是容易忽视而导致求解不完整的地方．
练习册系列答案
相关题目
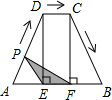（2013•河北）如图，梯形ABCD中，AB∥DC，DE⊥AB，CF⊥AB，且AE=EF=FB=5，DE=12动点P从点A出发，沿折线AD-DC-CB以每秒1个单位长的速度运动到点B停止．设运动时间为t秒，y=S△EPF，则y与t的函数图象大致是（ ）
（2013•河北）如图，四边形ABCD中，点M，N分别在AB，BC上，将△BMN沿MN翻折，得△FMN，若MF∥AD，FN∥DC，则∠B=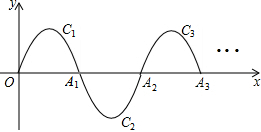
（2013•河北）如图，一段抛物线：y=-x（x-3）（0≤x≤3），记为C1，它与x轴交于点O，A1；
（2013•河北）如图，△OAB中，OA=OB=10，∠AOB=80°，以点O为圆心，6为半径的优弧