Question

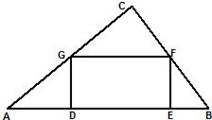
(本题8分)如图，在一块三角形区域ABC中，∠C=90°，边AC=8m，BC=6m，现要在△ABC内建造一个矩形水池DEFG，如图的设计方案是使DE在AB上．

1.（1）求△ABC中AB边上的高h；

2.（2）设DG=x，水池DEFG的面积为S，求S关于x的函数关系式，当x取何值时，水池DEFG的面积S最大？

 

Answer 1

 

1.（1）如图，作CH⊥AB于点H，交FG于点K．

由∠C=90°AC=8，BC=6，易得AB=10．∵S△ABC=  AC×BC=AB•CH，∴h=CH= 6×810=4.8．

2.如图，设DE=GF=y，∵GF∥AB，∴△CGF∽△CAB，由此可得 y:10=(4.8-x):4.8．∴ y=10- x

∴ S=xy=x(10-x)=- (x-2.4) ²+12．∵ a＜0，∴当x=2.4时，y有最大值12．

答：S= - (x-2.4) ²+12,当x取2.4m时，水池DEFG的面积S最大，且S=12m²．

解析:略