题目内容
已知:二次函数y=x2+bx+c的图象经过点A(0,-2)和点B(1,1),顶点为P.求:(1)这个二次函数的解析式;
(2)∠POA的正切值.
分析:(1)将点A(0,-2)和点B(1,1)代入二次函数y=x2+bx+c,即可求得解析式;
(2)根据顶点的公式得出点P的坐标,再根据三角函数的定义,求得∠POA的正切值.
(2)根据顶点的公式得出点P的坐标,再根据三角函数的定义,求得∠POA的正切值.
解答:解:(1)∵二次函数y=x2+bx+c的图象经过点A(0,-2)和点B(1,1),
∴
(2分)
解得
(2分)
∴所求二次函数的解析式为y=x2+2x-2.(1分)
(2)∵y=x2+2x-2=(x+1)2-3,
∴顶点P的坐标为(-1,-3).(3分)
∴tan∠POA=
.(2分)
∴
|
解得
|
∴所求二次函数的解析式为y=x2+2x-2.(1分)
(2)∵y=x2+2x-2=(x+1)2-3,
∴顶点P的坐标为(-1,-3).(3分)
∴tan∠POA=
| 1 |
| 3 |
点评:本题考查了用待定系数法球二次函数的解析式以及锐角三角函数的定义,是基础知识要熟练掌握.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 已知:二次函数的表达式为y=2x2+4x-1.
已知:二次函数的表达式为y=2x2+4x-1.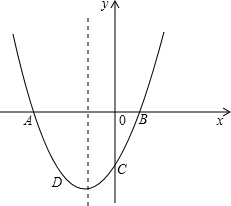 交于点C,点D(-2,-3)在抛物线上.
交于点C,点D(-2,-3)在抛物线上.