题目内容
 如图,等腰梯形ABCD中,AD∥BC,AB=5,BC=4,D点的坐标为(10,0),则C点的
如图,等腰梯形ABCD中,AD∥BC,AB=5,BC=4,D点的坐标为(10,0),则C点的
坐标为
- A.(6,3)
- B.(7,3)
- C.(6,4)
- D.(7,4)
D
分析:作BE垂直AD于E,CF垂直AD于F,设C的坐标为(x,y).根据等腰梯形的性质可求得AE=FD,从而分别求得AF,CF的值即可求得点C的坐标.
解答: 解:作BE垂直AD于E,CF垂直AD于F,设C的坐标为(x,y).已知在等腰梯形ABCD中,AD∥BC,AB=5,BC=4
解:作BE垂直AD于E,CF垂直AD于F,设C的坐标为(x,y).已知在等腰梯形ABCD中,AD∥BC,AB=5,BC=4
D点的坐标为(10,0),故AD=10.AE+FD=10-4=6,AE=FD=3,
故F的坐标为(7,0),所以C的坐标为(7,y)
又因为BE=CF,根据勾股定理求出BE=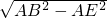 =4
=4
所以C的坐标为(7,4)
故选D.
点评:此题考查等腰梯形的性质及梯形中常见的辅助线的作法.
分析:作BE垂直AD于E,CF垂直AD于F,设C的坐标为(x,y).根据等腰梯形的性质可求得AE=FD,从而分别求得AF,CF的值即可求得点C的坐标.
解答:
 解:作BE垂直AD于E,CF垂直AD于F,设C的坐标为(x,y).已知在等腰梯形ABCD中,AD∥BC,AB=5,BC=4
解:作BE垂直AD于E,CF垂直AD于F,设C的坐标为(x,y).已知在等腰梯形ABCD中,AD∥BC,AB=5,BC=4D点的坐标为(10,0),故AD=10.AE+FD=10-4=6,AE=FD=3,
故F的坐标为(7,0),所以C的坐标为(7,y)
又因为BE=CF,根据勾股定理求出BE=
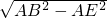 =4
=4所以C的坐标为(7,4)
故选D.
点评:此题考查等腰梯形的性质及梯形中常见的辅助线的作法.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 14、如图,等腰梯形ABCD中,AB∥CD,∠A=60°,BD平分∠ABC,若梯形ABCD的周长为40cm,则CD的长为( )
14、如图,等腰梯形ABCD中,AB∥CD,∠A=60°,BD平分∠ABC,若梯形ABCD的周长为40cm,则CD的长为( ) 24、已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC.
24、已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC. (2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=
(2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD= 如图,等腰梯形ABCD中,AD∥BC,AB=CD,对角线BD平分∠ABC,且BD⊥DC,上底AD=3cm.
如图,等腰梯形ABCD中,AD∥BC,AB=CD,对角线BD平分∠ABC,且BD⊥DC,上底AD=3cm. 如图,等腰梯形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥DC,延长BC到E,使CE=AD.
如图,等腰梯形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥DC,延长BC到E,使CE=AD.