Question

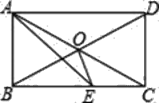
【题目】已知在平行四边形ABCD中，AB=6，BC=10，∠BAD=120°，E为线段BC上的一个动点（不与B，C重合），过E作直线AB的垂线，垂足为F，FE与DC的延长线相交于点G，

（1）如图1，当AE⊥BC时，求线段BE、CG的长度．

（2）如图2，点E在线段BC上运动时，连接DE，DF，△BEF与△CEG的周长之和是否是一个定值，若是请求出定值，若不是请说明理由．

（3）如图2，设BE=x，△DEF的面积为y，试求出y关于x的函数关系式．

Answer 1

【答案】（1）BE=3，EG =；（2）是定值，为15+5；（3）y=﹣x2+（0＜x＜10）．

【解析】

（1）先求出BE，AE，进而求出BF，EF，再用平行四边形的面积求出FG，即可得出结论；

（2）先求出BH，AH，再用相似表示出BF，EF，进而得出CG，EG，即可得出结论；

（3）利用三角形的面积公式即可得出结论．

（1）∵四边形ABCD是平行四边形，

∴AD∥BC，AB∥CD，

∴∠BAD+∠B=180°，

∵∠BAD=120°，

∴∠B=60°，

∵AE⊥BC于E，

在Rt△ABE中，∠BAE=30°，AB=6，

∴BE=3，AE=3，

∵EF⊥AB，

∴∠BFE=90°，

在Rt△BEF中，∠BEF=30°，

∴BF=BE=，EF=，

∵SABCD=BC×AE=AB×FG，

∴10×3=6FG，

∴FG=5，

∴EG=FG﹣EF=；

（2）如图2，

过点A作AH⊥BC于H，

∵∠B=60°，

∴BH=3，AH=3，

∵∠AHB=∠BFE=90°，∠B=∠B，

∴△ABH∽△EBF，

∴，

设BE=a，

∴，

∴BF=a，EF=a，

∵AB∥CD，

∴△BEF∽△CEG，

∴，

∴，

∴CG=（10﹣a），EG=（10﹣a），

∴C△BEF+C△CEG=BE+BF+EF+CE+CG+EG=a+a+a+10﹣a+（10﹣a）+（10﹣a）=10+5+5=15+5；

（3）同（2）的方法得，EF=x，CG=（10﹣x），

∴DG=CD+CG=6+5﹣x=11﹣x，

∴S△DEF=EF×DG=×x×（11﹣x）=﹣x2+（0＜x＜10）．