题目内容
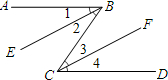已知：如图AB∥CD，BE∥CF．试说明：∠1=∠4．分析：根据两直线平行，内错角相等解答即可．
解答：解：∵AB∥CD，
∴∠ABC=∠BCD，
∵BE∥CF，
∴∠2=∠3，
∴∠ABC-∠2=∠BCD-∠3，
∴∠1=∠4．
∴∠ABC=∠BCD，
∵BE∥CF，
∴∠2=∠3，
∴∠ABC-∠2=∠BCD-∠3，
∴∠1=∠4．
点评：本题主要考查了两直线平行，内错角相等的性质，准确识图并熟记性质是解题的关键．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
5、已知，如图AB=CD，BC=AD，∠B=23°，则∠D=（ ）
24、完成下面的证明．
已知：如图AB∥CD，∠1=∠A，∠2=∠C，B、E、D在一条直线上．
21、填写下列推理中的空格
已知，如图AB∥CD，∠1=∠2，EP⊥FP，则以下错误的是（ ）