题目内容
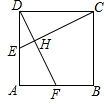（2011•盘锦）如图，在正方形ABCD中，点E、F分别为AD、AB的中点，连接DF、CE，DF与CE交于点H，则下列结论：①DF⊥CE；②DF=CE；③| DE |
| CE |
| HD |
| CD |
| DE |
| DC |
| HD |
| HE |
①②③
①②③
．分析：利用正方形的性质和已知条件可判定Rt△DAF≌Rt△DCE，有全等可判断①②是否正确，再利用相似三角形的判定方法证明△DHE∽△DAF，由相似三角形的性质可判断③④是否正确，进而可知正确结论的序号．
解答：解：∵四边形ABCD是正方形，
∴AB=BC=CD=DA，∠A=∠B=∠ADC=∠DCB=90°，
∵点E、F分别为AD、AB的中点，
∴DE=AE，
∴Rt△DAF≌Rt△DCE，
∴DF=CE，故②正确；
∠DEC=∠DFA，
∵∠DFA+∠FDA=90°，
∴∠DEC+∠FDA=90°，
∴∠DHE=90°，
即DF⊥CE，故①正确；
∵∠EDH=∠FDA，
∠A=∠DHE=90°，
∴△DHE∽△DAF，
∵
=
，
∵AB=BC=CD=DA，DF=CE，
∴
=
，故③正确；
∵
=
，
=
=
，
∴
≠
，故④不正确．
故答案为①②③．
∴AB=BC=CD=DA，∠A=∠B=∠ADC=∠DCB=90°，
∵点E、F分别为AD、AB的中点，
∴DE=AE，
∴Rt△DAF≌Rt△DCE，
∴DF=CE，故②正确；
∠DEC=∠DFA，
∵∠DFA+∠FDA=90°，
∴∠DEC+∠FDA=90°，
∴∠DHE=90°，
即DF⊥CE，故①正确；
∵∠EDH=∠FDA，
∠A=∠DHE=90°，
∴△DHE∽△DAF，
∵
| DH |
| AD |
| DE |
| DF |
∵AB=BC=CD=DA，DF=CE，
∴
| DE |
| CE |
| HD |
| CD |
∵
| DE |
| DC |
| 1 |
| 2 |
| HD |
| HE |
| DA |
| AF |
| 2 |
| 1 |
∴
| DE |
| DC |
| HD |
| HE |
故答案为①②③．
点评：本题考查了正方形的性质：四条边相等，四个角都是直角和全等三角形的判定以及全等三角形的性质；同时还考查了相似三角形的判定以及相似三角形的性质；难度不大，综合性不小．是一道考查学生基本能力不错的题目．
练习册系列答案
阅读快车系列答案
相关题目
线BD上．若AB=6m，AD=4m，设AM的长为xm，矩形AMPQ的面积为S平方米．
（2011•盘锦）如图，已知⊙O的半径为4，点D是直径AB延长线上一点，DC切⊙O于点C，连接AC，若∠CAB=30°，则BD的长为（ ）
（2011•盘锦）如图，矩形纸片ABCD，AD=2AB=4，将纸片折叠，使点C落在AD上的点E处，折痕为BF，则DE=