题目内容
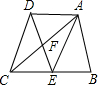 已知,如图,E、F分别为△ABC的边BC、CA的中点,延长EF到D,使得DF=EF,连接DA,DC,AE.
已知,如图,E、F分别为△ABC的边BC、CA的中点,延长EF到D,使得DF=EF,连接DA,DC,AE.(1)求证:四边形ABED是平行四边形;
(2)若AB=AC,试证明四边形AECD是矩形.
分析:(1)由已知可得:EF是△ABC的中位线,则可得EF∥AB,EF=
AB,又由DF=EF,易得AB=DE,根据有一组对边平行且相等的四边形是平行四边形,即可证得四边形ABED是平行四边形;
(2)由(1)可得四边形AECD是平行四边形,又由AB=AC,AB=DE,易得AC=DE,根据对角线相等的平行四边形是矩形,可得四边形AECD是矩形.
| 1 |
| 2 |
(2)由(1)可得四边形AECD是平行四边形,又由AB=AC,AB=DE,易得AC=DE,根据对角线相等的平行四边形是矩形,可得四边形AECD是矩形.
解答:证明:(1)∵E、F分别为△ABC的边BC、CA的中点,
∴EF∥AB,EF=
AB,(2分)
∵DF=EF,
∴EF=
DE,(3分)
∴AB=DE,(4分)
∴四边形ABED是平行四边形;(5分)
(2)∵DF=EF,AF=CF,
∴四边形AECD是平行四边形,(6分)
∵AB=AC,AB=DE,
∴AC=DE,(7分)
∴四边形AECD是矩形.(8分)
或∵DF=EF,AF=CF,
∴四边形AECD是平行四边形,(6分)
∵AB=AC,BE=EC,
∴∠AEC=90°,(7分)
∴四边形AECD是矩形.(8分)
∴EF∥AB,EF=
| 1 |
| 2 |
∵DF=EF,
∴EF=
| 1 |
| 2 |
∴AB=DE,(4分)
∴四边形ABED是平行四边形;(5分)
(2)∵DF=EF,AF=CF,
∴四边形AECD是平行四边形,(6分)
∵AB=AC,AB=DE,
∴AC=DE,(7分)
∴四边形AECD是矩形.(8分)
或∵DF=EF,AF=CF,
∴四边形AECD是平行四边形,(6分)
∵AB=AC,BE=EC,
∴∠AEC=90°,(7分)
∴四边形AECD是矩形.(8分)
点评:此题考查了平行四边形的判定(有一组对边平行且相等的四边形是平行四边形)、矩形的判定(对角线相等的平行四边形是矩形)以及三角形中位线的性质(三角形的中位线平行于三角形的第三边且等于第三边的一半).解题的关键是仔细分析图形,注意数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
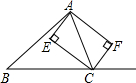 已知:如图,CE、CF分别是△ABC的内外角平分线,过点A作CE、CF的垂线,垂足分别为E、F.
已知:如图,CE、CF分别是△ABC的内外角平分线,过点A作CE、CF的垂线,垂足分别为E、F. 21、已知:如图,E,F分别是平行四边形ABCD的边AD,BC的中点.
21、已知:如图,E,F分别是平行四边形ABCD的边AD,BC的中点.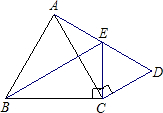 已知:如图,△BCE、△ACD分别是以BE、AD为斜边的直角三角形,且BE=AD,△CDE是等边三角形.求证:△ABC是等边三角形.
已知:如图,△BCE、△ACD分别是以BE、AD为斜边的直角三角形,且BE=AD,△CDE是等边三角形.求证:△ABC是等边三角形. 已知:如图,E,F分别是?ABCD的边AD,BC的中点.求证:AF=CE.
已知:如图,E,F分别是?ABCD的边AD,BC的中点.求证:AF=CE. 已知,如图,BE、CF分别是△ABC的边AC、AB上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.请你判断线段AD与AG有什么关系?并证明.
已知,如图,BE、CF分别是△ABC的边AC、AB上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.请你判断线段AD与AG有什么关系?并证明.