题目内容
 如图四边形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,P为AB边上的一动点,以PD,PC为边作平行四边形PCQD,则对角线PQ的长的最小值是
如图四边形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,P为AB边上的一动点,以PD,PC为边作平行四边形PCQD,则对角线PQ的长的最小值是
- A.3
- B.4
- C.5
- D.6
B
分析:在平行四边形PCQD中,设对角线PQ与DC相交于点G,可得G是DC的中点,过点Q作QH⊥BC,交BC的延长线于H,易证得Rt△ADP≌Rt△HCQ,即可求得BH=4,则可得当PQ⊥AB时,PQ的长最小,即为4;
解答: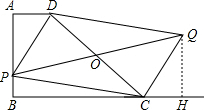 解:在平行四边形PCQD中,设对角线PQ与DC相交于点O,
解:在平行四边形PCQD中,设对角线PQ与DC相交于点O,
则O是DC的中点,
过点Q作QH⊥BC,交BC的延长线于H,
∵AD∥BC,
∴∠ADC=∠DCH,即∠ADP+∠PDG=∠DCQ+∠QCH,
∵PD∥CQ,
∴∠PDC=∠DCQ,
∴∠ADP=∠QCH,
又∵PD=CQ,
在Rt△ADP与Rt△HCQ中,
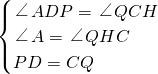
∴Rt△ADP≌Rt△HCQ(AAS),
∴AD=HC,
∵AD=1,BC=3,
∴BH=4,
∴当PQ⊥AB时,PQ的长最小,即为4.
故选B.
点评:本题考查了梯形的中位线的性质,梯形的中位线等于两底和的一半且平行于两底.
分析:在平行四边形PCQD中,设对角线PQ与DC相交于点G,可得G是DC的中点,过点Q作QH⊥BC,交BC的延长线于H,易证得Rt△ADP≌Rt△HCQ,即可求得BH=4,则可得当PQ⊥AB时,PQ的长最小,即为4;
解答:
 解:在平行四边形PCQD中,设对角线PQ与DC相交于点O,
解:在平行四边形PCQD中,设对角线PQ与DC相交于点O,则O是DC的中点,
过点Q作QH⊥BC,交BC的延长线于H,
∵AD∥BC,
∴∠ADC=∠DCH,即∠ADP+∠PDG=∠DCQ+∠QCH,
∵PD∥CQ,
∴∠PDC=∠DCQ,
∴∠ADP=∠QCH,
又∵PD=CQ,
在Rt△ADP与Rt△HCQ中,
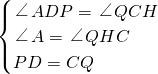
∴Rt△ADP≌Rt△HCQ(AAS),
∴AD=HC,
∵AD=1,BC=3,
∴BH=4,
∴当PQ⊥AB时,PQ的长最小,即为4.
故选B.
点评:本题考查了梯形的中位线的性质,梯形的中位线等于两底和的一半且平行于两底.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 17、如图四边形ABCD内接于⊙O,AB为直径,PD切⊙O于D,与BA延长线交于P点,已知∠BCD=130°,则∠ADP=
17、如图四边形ABCD内接于⊙O,AB为直径,PD切⊙O于D,与BA延长线交于P点,已知∠BCD=130°,则∠ADP= 如图四边形ABCD是边长为8的一个正方形,
如图四边形ABCD是边长为8的一个正方形,
 ( )
( ) 如图四边形ABCD中,AC平分∠BAD,CD∥AB,BC=6cm,∠BAD=30°,∠B=90°.则CD的长为
如图四边形ABCD中,AC平分∠BAD,CD∥AB,BC=6cm,∠BAD=30°,∠B=90°.则CD的长为 如图四边形ABCD中,CO=AO,BO=DO,AB与AD不相等,则图中有几对全等的三角形.( )
如图四边形ABCD中,CO=AO,BO=DO,AB与AD不相等,则图中有几对全等的三角形.( )