��Ŀ����
 ��2010•��������֪����OABC�Ķ���O��ƽ��ֱ������ϵ��ԭ�㣬��OA��OC�ֱ���x��y����������ϣ���OA=3cm��OC=4cm����M�ӵ�A������AB���յ�B�˶�����N�ӵ�C������CA���յ�A�˶�����M��Nͬʱ���������˶����ٶȾ�Ϊ1cm/�룬������һ���㵽���յ�ʱ����һ�㼴ֹͣ�˶������˶���ʱ��Ϊt�룮
��2010•��������֪����OABC�Ķ���O��ƽ��ֱ������ϵ��ԭ�㣬��OA��OC�ֱ���x��y����������ϣ���OA=3cm��OC=4cm����M�ӵ�A������AB���յ�B�˶�����N�ӵ�C������CA���յ�A�˶�����M��Nͬʱ���������˶����ٶȾ�Ϊ1cm/�룬������һ���㵽���յ�ʱ����һ�㼴ֹͣ�˶������˶���ʱ��Ϊt�룮��1������t��ʾ��N�����꣬��ָ��t��ȡֵ��Χ��
��2������������OAMN�����S��t�ĺ�����ϵʽ��
��3���Ƿ����ij��ʱ��t��ʹ�õ�O��N��M����ͬ��һ��ֱ���ϣ������ڣ������t��ֵ���������ڣ���˵�����ɣ�
��������1���������������AC��ֵ�����sin��AOC��ֵ����NE��OA��E���������������ε����ʾͿ��Ա�ʾ��NE��OE��ֵ���Ӷ����N������꣬��M�˶���ʱ��Ϳ������t�ķ�Χ��
��2����NF��AB��F������N�������Ϳ��Ա�ʾ��S��OAN��S��AMN���Ӷ�����������ۣ�
��3�����ݣ�2���Ľ���ʽ=S��OAM�������������t��ֵ�������Եó����ۣ�
��2����NF��AB��F������N�������Ϳ��Ա�ʾ��S��OAN��S��AMN���Ӷ�����������ۣ�
��3�����ݣ�2���Ľ���ʽ=S��OAM�������������t��ֵ�������Եó����ۣ�
����⣺��1����ͼ1����NE��OA��E��
���NEA=90�㣮
���ı���OABC�Ǿ��Σ�
���AOC=��B=90�㣬BC=OA��OC=AB��
��NE��OC��
��
=
��
��OA=3cm��OC=4cm����Rt��AOC�У��ɹ��ɶ�������
AC=5��
��CN=t��
��AN=5-t��
��
=
��
��NE=4-
t��
��tan��OAC=
=
��
��
=
��
��AE=3-
t��
��OE=
t��
��N��
t��4-
t����
��
=4��
��0��t��4��
��2����NF��AB��F��
���ı���AFNE�Ǿ��Σ�
��NF=AE��NE=AF��
��NF=3-
t��
��AM=t��
��S�ı���OAMN=
+
��
=
+
��
=-
t2+
t+6��
��3����O��N��M����ͬ��һ��ֱ����ʱ��
-
t2+
t+6=
��
��ã�t1=-2-2
����ȥ����t2=-2+2
��4��
��t��ֵΪ-2+2
��
���NEA=90�㣮
���ı���OABC�Ǿ��Σ�
���AOC=��B=90�㣬BC=OA��OC=AB��
��NE��OC��
��
| AN |
| AC |
| NE |
| OC |
��OA=3cm��OC=4cm����Rt��AOC�У��ɹ��ɶ�������
AC=5��
��CN=t��
��AN=5-t��
��
| 5-t |
| 5 |
| NE |
| 4 |
��NE=4-
| 4 |
| 5 |
��tan��OAC=
| EN |
| AE |
| 4 |
| 3 |
��
4-
| ||
| AE |
| 4 |
| 3 |

��AE=3-
| 3 |
| 5 |
��OE=
| 3 |
| 5 |
��N��
| 3 |
| 5 |
| 4 |
| 5 |
��
| AB |
| 1 |
��0��t��4��
��2����NF��AB��F��
���ı���AFNE�Ǿ��Σ�
��NF=AE��NE=AF��

��NF=3-
| 3 |
| 5 |
��AM=t��
��S�ı���OAMN=
| OA��NE |
| 2 |
| AM��NF |
| 2 |
=
3(4-
| ||
| 2 |
t(3-
| ||
| 2 |
=-
| 3 |
| 10 |
| 3 |
| 10 |
��3����O��N��M����ͬ��һ��ֱ����ʱ��
-
| 3 |
| 10 |
| 3 |
| 10 |
| 3��t |
| 2 |
��ã�t1=-2-2
| 6 |
| 6 |
��t��ֵΪ-2+2
| 6 |
���������⿼���˾��ε����ʵ����ã�ƽ���߷��߶γɱ������������ã��������ı��ε���������ã������ε���������ã����Ǻ���ֵ�����ã����ʱÿһ��֮���ǵݽ���ϵ����Ҫ�������⣬��һ���

��ϰ��ϵ�д�
�����Ŀ
 ��2010•��������֪��Rt��ABC�У���C=90�㣬��E�ڱ�AB�ϣ���AE=AC����BAC��ƽ����AD��BC���ڵ�D��
��2010•��������֪��Rt��ABC�У���C=90�㣬��E�ڱ�AB�ϣ���AE=AC����BAC��ƽ����AD��BC���ڵ�D��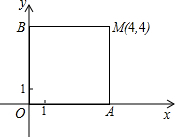 ��2010•��������֪������������ͼ����㣨-2��-2����
��2010•��������֪������������ͼ����㣨-2��-2����