题目内容
在△ABC中，若BC=
，AB=
，AC=3，则cosA= ．
| 2 |
| 7 |
考点：解直角三角形
专题：
分析：根据勾股定理的逆定理得出△ABC为直角三角形，再根据余弦函数的定义得出答案即可．
解答：解：∵BC=
，AB=
，AC=3，
∴（
）2+（
）2=32，
∴BC2+AB2=AC2，
∴△ABC为直角三角形，
∴cosA=
=
，
故答案为
．
| 2 |
| 7 |
∴（
| 2 |
| 7 |
∴BC2+AB2=AC2，
∴△ABC为直角三角形，
∴cosA=
| AB |
| AC |
| ||
| 3 |
故答案为
| ||
| 3 |
点评：本题考查了解直角三角形以及勾股定理的逆定理，熟记三角函数的求法是解题的关键．
练习册系列答案
相关题目
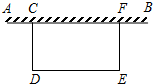如图，某校广场有一段25米差个的旧围栏，现打算利用该围栏的一部分（或全部）为一边，围成一块100平方米的长方形草坪（如图CDEF，CD＜CF）已知整修旧围栏的价格是每米1.75元，建新围栏的价格是4.5元．若CF=x米，计划修建费为y元．
如图，A、B、C、D为矩形的四个顶点，AB=16cm，BC=6cm，动点P、Q分别从点A、C同时出发，点P以3cm/s的速度向点B移动，点Q以2cm/s的速度向点D移动．当点P运动到点B停止时，点Q也随之停止运动．
如图，在△ABC中，∠A=40°，将△ABC延虚线剪去∠A，则∠1+∠2等于（ ）| A、180° | B、200° |
| C、220° | D、270° |