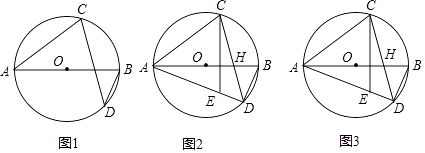
ћвƒњƒЏ»Ё
°Њћвƒњ°њ»зЌЉ£ђ‘Џ∆љ√ж÷±љ«„ш±кѕµ÷–£ђ÷±ѕяy=©Б ![]() x©Б
x©Б ![]() ”лx÷бљї”ЏµгA£ђ”лy÷бљї”ЏµгC£ђ≈„ќпѕяy=ax2©Б
”лx÷бљї”ЏµгA£ђ”лy÷бљї”ЏµгC£ђ≈„ќпѕяy=ax2©Б ![]() x+c£®a°ў0£©Њ≠єэA£ђB£ђC»эµг£Ѓ
x+c£®a°ў0£©Њ≠єэA£ђB£ђC»эµг£Ѓ
£®1£©«уєэA£ђB£ђC»эµг≈„ќпѕяµƒљвќц љ≤Ґ«у≥цґ•µгFµƒ„ш±к£ї
£®2£©‘Џ≈„ќпѕя…ѕ «Јсіж‘ЏµгP£ђ є°чABPќ™÷±љ«»эљ«–ќ£њ»фіж‘Џ£ђ÷±љ”–і≥цPµг„ш±к£ї»ф≤їіж‘Џ£ђ«лЋµ√чјн”…£ї
£®3£© ‘ћљЊњ‘Џ÷±ѕяAC…ѕ «Јсіж‘Џ“їµгM£ђ єµ√°чMBFµƒ÷№≥§„о–°£њ»фіж‘Џ£ђ«у≥цMµгµƒ„ш±к£ї»ф≤їіж‘Џ£ђ«лЋµ√чјн”…£Ѓ
°Њір∞Є°њ
£®1£©
љв£Ї°я÷±ѕяy=©Б ![]() x©Б
x©Б ![]() ”лx÷бљї”ЏµгA£ђ”лy÷бљї”ЏµгC
”лx÷бљї”ЏµгA£ђ”лy÷бљї”ЏµгC
°аµгA£®©Б1£ђ0£©£ђC£®0£ђ©Б ![]() £©
£©
°яµгA£ђCґЉ‘Џ≈„ќпѕя…ѕ£ђ
°а 
°а 
°а≈„ќпѕяµƒљвќц љќ™y= ![]() x2©Б
x2©Б ![]()
![]() x©Б
x©Б ![]()
°аґ•µгF£®1£ђ©Б ![]() £©
£©
£®2£©
љв£ЇЈљЈ®“ї£Їіж‘Џ£Ї
p1£®0£ђ©Б ![]() £©£ђp2£®2£ђ©Б
£©£ђp2£®2£ђ©Б ![]() £©
£©
ЈљЈ®ґю£Ї
…иP£®t£ђ ![]() £©£ђA£®©Б1£ђ0£©£ђB£®3£ђ0£©£ђ
£©£ђA£®©Б1£ђ0£©£ђB£®3£ђ0£©£ђ
°яPA°ЌPB£ђ°аKPA°ЅKPB=©Б1£ђ
![]() =©Б1£ђ
=©Б1£ђ
°а£®t+1£©£®t©Б3£©=©Б3£ђ°аt1=0£ђt2=2£ђ
°аP1£®0£ђ©Б ![]() £©£ђP2£®2£ђ©Б
£©£ђP2£®2£ђ©Б ![]() £©£Ѓ
£©£Ѓ
£®3£©
љв£Їіж‘Џ
јн”…£Ї
љвЈ®“ї£Ї
—”≥§BCµљµгB°д£ђ єB°дC=BC£ђЅђљ”B°дFљї÷±ѕяAC”ЏµгM£ђ‘тµгMЊЌ «Ћщ«уµƒµг£ђ
°яєэµгB°д„чB°дH°ЌAB”ЏµгH£ђ
°яBµг‘Џ≈„ќпѕяy= ![]() x2©Б
x2©Б ![]()
![]() x©Б
x©Б ![]() …ѕ£ђ
…ѕ£ђ
°аB£®3£ђ0£©£ђ
‘ЏRt°чBOC÷–£ђtan°ѕOBC= ![]()
°а°ѕOBC=30°г£ђBC=2 ![]()
‘ЏRt°чB°дBH÷–£ђB°дH= ![]() BB°д=2
BB°д=2 ![]()
BH= ![]() B°дH=6£ђ°аOH=3£ђ
B°дH=6£ђ°аOH=3£ђ
°аB°д£®©Б3£ђ©Б2 ![]() £©£Ѓ
£©£Ѓ
…и÷±ѕяB°дFµƒљвќц љќ™y=kx+b£ђ
°а  £ђ
£ђ
љвµ√  £ђ
£ђ
°аy= ![]() £Ѓ
£Ѓ
 £ђ
£ђ
љвµ√  £ђ
£ђ
°аM£® ![]() £©
£©
°а‘Џ÷±ѕяAC…ѕіж‘ЏµгM£ђ єµ√°чMBFµƒ÷№≥§„о–°£ђіЋ ±M£® ![]() £©£Ѓ
£©£Ѓ
љвЈ®ґю£Ї
єэµгF„чACµƒієѕяљїy÷б”ЏµгH£ђ‘тµгHќ™µгFєЎ”Џ÷±ѕяACµƒґ‘≥∆µг£ђЅђљ”BHљїAC”ЏµгM£ђ‘тµгM
Љіќ™Ћщ«у£Ѓ
єэµгF„чFG°Ќy÷б”ЏµгG£ђ‘тOB°ќFG£ђBC°ќFH£ђ
°а°ѕBOC=°ѕFGH=90°г£ђ°ѕBCO=°ѕFHG
°а°ѕHFG=°ѕCBO
ЌђЈљЈ®“їњ…«уµ√B£®3£ђ0£©
‘ЏRt°чBOC÷–£ђtan°ѕOBC= ![]()
°а°ѕOBC=30°г£ђњ…«уµ√GH=GC= ![]()
°аGFќ™ѕяґќCHµƒіє÷±∆љЈ÷ѕя£ђњ…÷§µ√°чCFHќ™µ»±я»эљ«–ќ
°аACіє÷±∆љЈ÷FH
ЉіµгHќ™µгFєЎ”ЏACґ‘≥∆µг£ђ
°аH£®0£ђ©Б ![]() £©
£©
…и÷±ѕяBHµƒљвќц љќ™y=kx+b£ђ”…ћв“вµ√£ђ  £ђ
£ђ
љвµ√  £ђ
£ђ
°аy= ![]() £ђ
£ђ
 £ђ
£ђ
љвµ√  £ђ
£ђ
°аM£® ![]() £©£ђ
£©£ђ
°а‘Џ÷±ѕяAC…ѕіж‘ЏµгM£ђ єµ√°чMBFµƒ÷№≥§„о–°£ђіЋ ±M£® ![]() £©
£©



°Њљвќц°њ£®1£©≈„ќпѕяљвќц љ÷–”–ЅљЄціэґ®ѕµ эa£ђc£ђЄщЊЁ÷±ѕяACљвќц љ«уµгA°ҐC„ш±к£ђіъ»л≈„ќпѕяљвќц љЉіњ…£ї£®2£©Ј÷ќц≤їƒ—ЈҐѕ÷£ђ°чABPµƒ÷±љ«ґ•µг÷їњ…ƒ№ «P£ђЄщЊЁ“—÷™ћхЉюњ…÷§AC2+BC2=AB2 £ђ є µгC¬ъ„гћв“в£ђЄщЊЁ≈„ќпѕяµƒґ‘≥∆–‘£ђµгCєЎ”Џ≈„ќпѕяґ‘≥∆÷бµƒґ‘≥∆µг“≤ЈыЇѕћв“в£ї£®3£©”…”ЏB£ђF «ґ®µг£ђBFµƒ≥§“їґ®£ђ µЉ …ѕЊЌ ««уBM+FM„о–°£ђ’“≥цµгBєЎ”Џ÷±ѕяACµƒґ‘≥∆µгB'£ђЅђљ”B'F£ђљїAC”ЏµгM£ђµгMЉіќ™Ћщ«у£ђ”…£®2£©њ…÷™£ђBC°ЌAC£ђ—”≥§BCµљB'£ђ єBC=B'C£ђјы”√÷–ќїѕяµƒ–‘÷ њ…µ√B'µƒ„ш±к£ђі”ґшњ…«у÷±ѕяB'Fµƒљвќц љ£ђ‘ў”л÷±ѕяACµƒљвќц љЅ™ЅҐ£ђњ…«уMµг„ш±к£Ѓ
°ЊњЉµгЊЂќц°њјы”√ґюіќЇѓ эµƒЌЉѕуЇЌґюіќЇѓ эµƒ–‘÷ ґ‘ћвƒњљш––≈–ґѕЉіњ…µ√µљір∞Є£ђ–и“™ м÷™ґюіќЇѓ эЌЉѕсєЎЉьµг£Ї1°Ґњ™њЏЈљѕт2°Ґґ‘≥∆÷б 3°Ґґ•µг 4°Ґ”лx÷бљїµг 5°Ґ”лy÷бљїµг£ї‘цЉх–‘£Їµ±a>0 ±£ђґ‘≥∆÷б„у±я£ђyЋжx‘ціуґшЉх–°£їґ‘≥∆÷б”“±я£ђyЋжx‘ціуґш‘ціу£їµ±a<0 ±£ђґ‘≥∆÷б„у±я£ђyЋжx‘ціуґш‘ціу£їґ‘≥∆÷б”“±я£ђyЋжx‘ціуґшЉх–°£Ѓ