Question

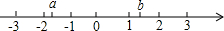运算基础
①计算：(

2

+

3

+

5

)(3

2

+2

3

-

30

)
②已知a、b在数轴上的位置如图所示，化简：

(a+1)2

+

(b+1)2

-

(a-b)2

③解方程：x2-2

5

x+5=0
④已知两个连续奇数的乘积是143，求这两个数．

Answer 1

分析：①直接利用乘法分配律即可求出答案；
②根据所给数轴，继而将所给式子化简得出答案．
③利用配方法即可解出方程的解；
④设其中一个奇数为x，则与其连续的奇数为x+2，根据题意有x（x+2）=143，即可解得答案．

解答：解：①原式=6+2

6

-2

15

+3

6

+6-3

10

+3

10

+2

15

-5

6

=12-2

6

；
②由题意知：a＜-1＜0＜1＜b，
∴原式=|a+1|+|b+1|-|a-b|=-a-1+b+1-b+a=0；
③原方程可变为：（x-

5

）²=0，
解得：x-

5

=0，x=

5

．
④设其中一个奇数为x，则与其连续的奇数为x+2，根据题意有x（x+2）=143，
解得：x=11，
即这两个数为11和13．

点评：本题考查了二次根式的混合运算，数轴及二次根式的性质与化简的知识，属于基础题，注意细心运算．