题目内容
二次函数 的图像的顶点为
的图像的顶点为 ,与
,与 轴交于点
轴交于点 ,以
,以 为边在第二象限内作等边三角形
为边在第二象限内作等边三角形 .
.

(1)求直线 的表达式和点
的表达式和点 的坐标;
的坐标;
(2)点 在第二象限,且△
在第二象限,且△ 的面积等于△
的面积等于△ 的面积,求点
的面积,求点 的坐标;
的坐标;
(3)以 轴上的点
轴上的点 为圆心,1为半径的圆,与以点
为圆心,1为半径的圆,与以点 为圆心,
为圆心, 的长为半径的圆相切,直接写出点
的长为半径的圆相切,直接写出点 的坐标.
的坐标.
(1) ,
, (2)
(2) (3)
(3) ,
, ,
, ,
,
【解析】解:(1)二次函数 的图像的顶点
的图像的顶点 ,与
,与 轴的交点
轴的交点 ,
(2分)
,
(2分)
设直线 的表达式为
的表达式为 ,
,
可求得 ,
, .所以直线
.所以直线 的表达式为
的表达式为 . (1分)
. (1分)
可得 ,∵
,∵ ,
,
∴ .
(1分)
.
(1分)
在Rt△ 中,由勾股定理得:
中,由勾股定理得: .
.
∴ .点
.点 .
(1分)
.
(1分)
解:(2)∵点 、
、 都在第二象限,且△
都在第二象限,且△ 的面积等于△
的面积等于△ 的面积,
的面积,
∴ ∥
∥ .
(1分)
.
(1分)
设直线 的表达式为
的表达式为 ,点
,点 在直线
在直线 上,
上,
可得  .
.
∴直线 的表达式为
的表达式为 .
(1分)
.
(1分)
可得点 的坐标:
的坐标: .
(1分)
.
(1分)
解:(3)点 的坐标
的坐标 ,
, ,
, ,
, .
.
(1)已知抛物线的解析式,其顶点以及函数图象与y轴交点坐标易求得.在求点C的坐标时,要把握住Rt△AOB的特殊性(含30°角),显然,若△ABC是等边三角形,那么AC与x轴垂直,无论通过勾股定理求边长还是根据B点在AC的中垂线上,都能比较容易的求出点C的坐标.
(2)“M点在第二象限内”确定了点M的大致范围,若“△ABM的面积等于△ABC的面积”,以AB为底边进行分析,那么点C、点M到直线AB的距离是相同的,即CM∥AB,直线AB的解析式易求,两直线平行则斜率相同,再代入点C的坐标就能通过待定系数法求出直线CM的解析式,然后代入点M的纵坐标即可得出结论.
(3)首先求出⊙C的半径,即CM的长.若⊙C与⊙N相切,就要分两种情况来考虑:①外切,CN长等于两圆的半径和;②内切,CN长等于两圆的半径差.
在明确CN长的情况下,在Rt△CAN中,通过勾股定理求出AN的长,进一步即可确定点N的坐标.




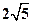 的
的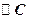 与x轴交于
与x轴交于 、
、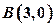 两点,且点C在x轴的上方.
两点,且点C在x轴的上方.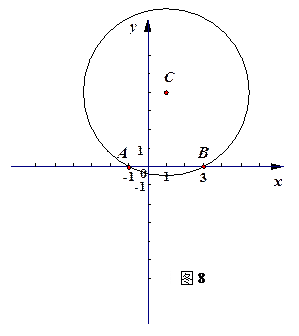

 、B、C,求这二次函数的解析式;
、B、C,求这二次函数的解析式; M、A、B为顶点的四边形是平行四边形,请你直接写出点M的坐标.
M、A、B为顶点的四边形是平行四边形,请你直接写出点M的坐标. 的
的 与x轴交于
与x轴交于 、
、 两点,且点C在x轴的上方.
两点,且点C在x轴的上方.

 、B、C,求这二次函数的解析式;
、B、C,求这二次函数的解析式;