题目内容
已知m，n是关于x的方程x2-2ax+a+6=0的两实根，求y=（m-1）2+（n-1）2的最小值．
解：依题意△=4a2-4（a+6）≥0，
即a2-a-6≥0，
∴a≤-2或a≥3，
由m+n=2a，mn=a+6，
y=m2+n2-2（m+n）+2
=（m+n）2-2mn-2（m+n）+2
=4a2-6a-10，
=4（a-
）2-
，
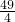∴a=3时，y的最小值为8．
故y的最小值为8．
分析：根据方程有两个根，利用根的判别式求出a的取值范围，再根据根与系数的关系求出m+n与mn的值，然后把y=（m-1）2+（n-1）2整理成m+n与mn的形式，代入进行计算即可求解．
点评：本题考查了二次函数的最值问题，根与系数的关系，根的判别式，利用根的判别式求出a的取值范围是解题的关键，也是同学们容易出错的地方．
即a2-a-6≥0，
∴a≤-2或a≥3，
由m+n=2a，mn=a+6，
y=m2+n2-2（m+n）+2
=（m+n）2-2mn-2（m+n）+2
=4a2-6a-10，
=4（a-
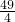）2-，∴a=3时，y的最小值为8．
故y的最小值为8．
分析：根据方程有两个根，利用根的判别式求出a的取值范围，再根据根与系数的关系求出m+n与mn的值，然后把y=（m-1）2+（n-1）2整理成m+n与mn的形式，代入进行计算即可求解．
点评：本题考查了二次函数的最值问题，根与系数的关系，根的判别式，利用根的判别式求出a的取值范围是解题的关键，也是同学们容易出错的地方．
练习册系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
已知x1、x2是关于x的一元二次方程x2-（2m+3）x+m2=0的两个不相等的实数根，且满足x1+x2=m2，则m的值是（ ）
| A、-1 | B、3 | C、3或-1 | D、-3或1 |