题目内容
18、如图，从四边形的一个顶点出发，可以连1条对角线，四边形被分成两个三角形，从五边形的一个顶点出发，可以连2条对角线，五边形被分成3个三角形，从六边形的一个顶点出发，可以连3条对角线，六边形被分成4个三角形，按照这个规律，从n边形的一个顶点出发，可以连
n-3
条对角线，n边形被分成n-2
个三角形．分析：由已知观察、分析
四边形：对角线数1=4-3三角形个数2=4-2（可以认为对角线条数是边数-3，三角形个数边数-2）．
五边形：对角线数2=5-3三角形个数3=5-2（同样是对角线条数是边数-3，三角形个数边数-2）．
再看六边形：对角线数3=6-3三角形个数4=6-2（同样是对角线条数是边数-3，三角形个数边数-2）．
由此可得出规律．
四边形：对角线数1=4-3三角形个数2=4-2（可以认为对角线条数是边数-3，三角形个数边数-2）．
五边形：对角线数2=5-3三角形个数3=5-2（同样是对角线条数是边数-3，三角形个数边数-2）．
再看六边形：对角线数3=6-3三角形个数4=6-2（同样是对角线条数是边数-3，三角形个数边数-2）．
由此可得出规律．
解答：解：四边形：对角线数1=4-3三角形个数2=4-2
五边形：对角线数2=5-3三角形个数3=5-2
六边形：对角线数3=6-3三角形个数4=6-2
…
n变形：对角线数n-3三角形个数n-2
故答案为：n-3，n-2．
五边形：对角线数2=5-3三角形个数3=5-2
六边形：对角线数3=6-3三角形个数4=6-2
…
n变形：对角线数n-3三角形个数n-2
故答案为：n-3，n-2．
点评：此题主要考查了学生观察问题，总结规律的能力培养．关键是能够得到规律：从一个多边形一个顶点出发，可以连的对角线的条数是边数-3，分成的三角形数是边数-2．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
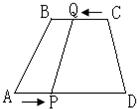13、如图：在四边形ABCD中，AD∥BC，且AD＞BC，BC=6cm，AD=9cm，P、Q分别从A、C同时出发，P以1cm/s的速度由A向D运动，Q以2cm/s的速度由C向B运动，
≈1.41]
...