题目内容
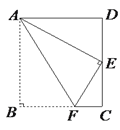
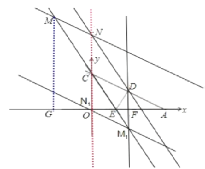
【题目】如图,Rt△OAC是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点C在y轴上,OA和OC是方程x![]() (3+
(3+![]() )x+3
)x+3![]() =0的两根(OA>OC),∠CAO=30°,将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.
=0的两根(OA>OC),∠CAO=30°,将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.
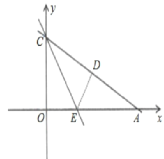
(1)求点D的坐标;
(2)设点M为直线CE上的一点,过点M作AC的平行线,交y轴于点N,是否存在这样的点M,使得以M、N、D. C为顶点的四边形是平行四边形?若存在,请求出符合条件的点M的坐标;若不存在,请说明理由.
【答案】(1)D(![]() ,
,![]() );(2)M(
);(2)M(![]() ,
,![]() );
);
【解析】
(1)由折纸可以知道CD=OC,从而求出AD,作DF⊥OA于F解直角三角形可以求出D点的坐标.
(2)存在满足条件的M点,利用三角形全等和平行线等分线段定理可以求出M点对应的坐标.
(1) 解方程x![]() (3+
(3+![]() )x+3
)x+3![]() =0得:
=0得:
x![]() =
=![]() ,x
,x![]() =3
=3
∵OA>OC
∴OA=3,OC=![]() ;
;
在Rt△AOC中,由勾股定理得:
AC=![]() =2
=2![]() ,
,
由轴对称得:CO=CD=![]() ,作DF⊥OA于F,
,作DF⊥OA于F,
∴AD=![]() ,作DF⊥OA,且∠CAO=30°,
,作DF⊥OA,且∠CAO=30°,
∴DF=![]() ,由勾股定理得:
,由勾股定理得:
AF=![]() ,
,
∴OF=![]() ,∴OF=AF
,∴OF=AF
∴D(![]() ,
,![]() );
);
(2)∵M![]() N
N![]()
∠N![]() M
M![]() F=∠ADF,∠FN
F=∠ADF,∠FN![]() M
M![]() =∠FAD
=∠FAD
∵OF=AF
∴△ADF≌△N![]() M
M![]() F(AAS),
F(AAS),
∴M![]() F=DF=
F=DF=![]() ,N
,N![]() F=AF=
F=AF=![]() ,
,
∴M![]() (
(![]() ,
, ![]() ),作MG⊥OA,
),作MG⊥OA,
∵四边形MCDN和四边形CN![]() M
M![]() D是平行四边形
D是平行四边形
∴MC=ND,ND=CM![]() ∴MC=CM
∴MC=CM![]()
∴GO=OF=![]() ,OE=1
,OE=1
∴GE=![]() ,
,
∴EOC△∽△EGM
∴![]()
∴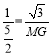 解得:
解得:
MG=![]() ,
,
∴M(![]() ,
,![]() )
)

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目