题目内容
在直角坐标系中,二次函数y=-| 1 |
| 2 |
| 3m |
| 2 |
| OC |
| OA |
| OC |
| OB |
| 2 |
| 5 |
(1)求△ABC的面积及这个二次函数的具体表达式;
(2)试设计满足下述条件的一个方案(说明理由):保持图象的形状大小不变,使以图象与坐标轴的3个交点为顶点的三角形的面积是△ABC的面积的一半.
分析:(1)设出ABC三点的坐标,用n表示出ab,c;由勾股定理可得答案;
(2)保持图象的张口和顶点的纵坐标不变,保持图象的对称轴与y轴平行,平移图象,使图象与y轴的交点C′坐标为(0,1),则这个图象为所求.
(2)保持图象的张口和顶点的纵坐标不变,保持图象的对称轴与y轴平行,平移图象,使图象与y轴的交点C′坐标为(0,1),则这个图象为所求.
解答:解:
(1)设点A(a,0),B(b,0),C(0,c)其中(a<0,b>0,c>0),
由条件得,c=n-5,ab=-2(n-5).
在Rt△ABC中,∵CO⊥AB,有
=
,
∴CO2=AO•BO,
∴(n-5)2=-ab,
故(n-5)2=2(n-5),
解得n=7或n=5(舍去),
从而c=2,
因为
+
=
,
=
,
于是,
+
=
,
解得a=-1或a=-4,
因OC>OA,
故舍去a=-4,
由a=-1,求得b=4,
故S△ABC=
•OC•AB=5,
又因为点A(-1,0)在抛物线上,
所以把x=-1,y=0代入y=-
x2+
x+2,得m=1,
所以y=-
x2+
x+2;
(2)参考方案:保持图象的张口和顶点的纵坐标不变,保持图象的对称轴与y轴平行,平移图象,使图象与y轴的交点C′坐标为(0,1),
则这个图象为所求,理由如下:由y=-
x2+
x+2=-
(x-
)2+
,
设移动后的抛物线为y=-
(x-k)2+
,则这图象的形式、大小保持不变,
又设这图象过点C′(0,1),把x=0,y=1代入上式,
求得k=±
,
所求的抛物线为y=-
(x-
)2+
①或y=-
(x+
)2+
②
设①与x轴的交点为A′,B′,其横坐标分别为x1,x2(x1≤x2),
则x1,x2为方程-
(x-
)2+
=0的两根,
解这个方程得x1=
-
,x2=
+
,
∴|x1-x2|=5,所以A′B′=5,
∴S△A′B′C′=
S△ABC,同理对于②也成立.
(1)设点A(a,0),B(b,0),C(0,c)其中(a<0,b>0,c>0),
由条件得,c=n-5,ab=-2(n-5).
在Rt△ABC中,∵CO⊥AB,有
| CO |
| AO |
| BO |
| CO |
∴CO2=AO•BO,
∴(n-5)2=-ab,
故(n-5)2=2(n-5),
解得n=7或n=5(舍去),
从而c=2,
因为
| CO |
| AO |
| CO |
| BO |
| 2 |
| 5 |
| CO |
| AO |
| BO |
| CO |
于是,
| 2 |
| -a |
| -a |
| 2 |
| 2 |
| 5 |
解得a=-1或a=-4,
因OC>OA,
故舍去a=-4,
由a=-1,求得b=4,
故S△ABC=
| 1 |
| 2 |
又因为点A(-1,0)在抛物线上,
所以把x=-1,y=0代入y=-
| 1 |
| 2 |
| 3m |
| 2 |
所以y=-
| 1 |
| 2 |
| 3 |
| 2 |
(2)参考方案:保持图象的张口和顶点的纵坐标不变,保持图象的对称轴与y轴平行,平移图象,使图象与y轴的交点C′坐标为(0,1),
则这个图象为所求,理由如下:由y=-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 25 |
| 8 |
设移动后的抛物线为y=-
| 1 |
| 2 |
| 25 |
| 8 |
又设这图象过点C′(0,1),把x=0,y=1代入上式,
求得k=±
| ||
| 2 |
所求的抛物线为y=-
| 1 |
| 2 |
| ||
| 2 |
| 25 |
| 8 |
| 1 |
| 2 |
| ||
| 2 |
| 25 |
| 8 |
设①与x轴的交点为A′,B′,其横坐标分别为x1,x2(x1≤x2),
则x1,x2为方程-
| 1 |
| 2 |
| ||
| 2 |
| 25 |
| 8 |
解这个方程得x1=
| ||
| 2 |
| 5 |
| 2 |
| ||
| 2 |
| 5 |
| 2 |
∴|x1-x2|=5,所以A′B′=5,
∴S△A′B′C′=
| 1 |
| 2 |
点评:本题考查学生将二次函数的图象与解析式相结合处理问题、解决问题的能力.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 如图,在直角坐标系中,二次函数的顶点为C(4,-3),且在x轴上截得的线段AB=6,则二次函数的表达式为
如图,在直角坐标系中,二次函数的顶点为C(4,-3),且在x轴上截得的线段AB=6,则二次函数的表达式为

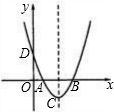
 (2012•青神县一模)如图,在直角坐标系中,二次函数y=ax2+bx+c(a>0)的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),OB=OC,tan∠ACO=
(2012•青神县一模)如图,在直角坐标系中,二次函数y=ax2+bx+c(a>0)的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),OB=OC,tan∠ACO=