题目内容
 如图,以正方形ABCD的对角线AC为一边作菱形AEFC,则∠CFA=( )
如图,以正方形ABCD的对角线AC为一边作菱形AEFC,则∠CFA=( )分析:根据正方形的对角线平分一组对角可得∠ACD=45°,根据菱形的四条边都相等可得AC=CF,再根据等边对等角可得∠CAF=∠CFA,然后利用三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
解答:解:在正方形ABCD中,∠ACD=45°,
在菱形AEFC中,AC=CF,
所以,∠CAF=∠CFA,
由三角形的外角性质,∠CAF+∠CFA=∠ACD=45°,
所以,∠CFA=
∠ACD=
×45°=22.5°.
故选C.
在菱形AEFC中,AC=CF,
所以,∠CAF=∠CFA,
由三角形的外角性质,∠CAF+∠CFA=∠ACD=45°,
所以,∠CFA=
| 1 |
| 2 |
| 1 |
| 2 |
故选C.
点评:本题考查了正方形的对角线平分一组对角的性质,菱形的四条边都相等的性质,以及三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质是解题的关键.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 13、如图,以直角△ABC的三边向外作正方形,其面积分别为S1,S2,S3且S1=4,S2=8,则S3=
13、如图,以直角△ABC的三边向外作正方形,其面积分别为S1,S2,S3且S1=4,S2=8,则S3=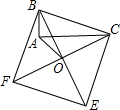 如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6
如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6 如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连接AO,如果AB=3,AO=
如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连接AO,如果AB=3,AO= 如图,以Rt△ABC的斜边和一直角边为边长向外作正方形,面积分别为169和25,则另一直角边的长度BC为( )
如图,以Rt△ABC的斜边和一直角边为边长向外作正方形,面积分别为169和25,则另一直角边的长度BC为( ) 如图,以Rt△ABC各边为边长的正方形面积分别为S1、S2、S3,且S1+S2+S3=50,则AB=( )
如图,以Rt△ABC各边为边长的正方形面积分别为S1、S2、S3,且S1+S2+S3=50,则AB=( )