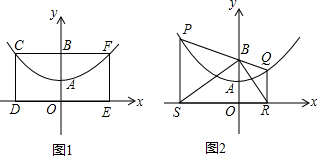
题目内容
如图1,已知抛物线的顶点为![]() ,且经过原点
,且经过原点![]() ,与
,与![]() 轴的另一个交点为
轴的另一个交点为![]() .
.
1.求抛物线的解析式;
2.若点![]() 在抛物线的对称轴上,点
在抛物线的对称轴上,点![]() 在抛物线上,且以
在抛物线上,且以![]() 、
、![]() 、
、![]() 、
、![]() 四点为顶点的四边形为平行四边形,求
四点为顶点的四边形为平行四边形,求![]() 点的坐标;
点的坐标;
3.连接![]() 、
、![]() ,如图2,在
,如图2,在![]() 轴下方的抛物线上是否存在点
轴下方的抛物线上是否存在点![]() ,使得
,使得![]() 与
与![]() 相似?若存在,求出
相似?若存在,求出![]() 点的坐标;若不存在,说明理由.
点的坐标;若不存在,说明理由.
1.
 抛物线的解析式为
抛物线的解析式为![]() ,
,
即![]() .
.
2.
如图1,当四边形![]() 是平行四边形时,
是平行四边形时,
 .
.
由![]() ,得
,得![]() ,
,![]() ,
,
 ,
,![]() .
.
 点的横坐标为
点的横坐标为![]() .
.
将![]() 代入
代入![]() ,
,
得![]() ,
,![]() ;
;
根据抛物线的对称性可知,在对称轴的左侧抛物线上存在点![]() ,使得四边形
,使得四边形![]() 是平行四边形,此时
是平行四边形,此时![]() 点的坐标为
点的坐标为![]() .
.
当四边形![]() 是平行四边形时,
是平行四边形时,![]() 点即为
点即为![]() 点,此时
点,此时![]() 点的坐标为
点的坐标为![]()
3.
如图2,由抛物线的对称性可知:
 ,
,![]() .
.
若![]() 与
与![]() 相似,
相似,
必须有![]() .
.
设![]() 交抛物线的对称轴于
交抛物线的对称轴于![]() 点,
点,
显然![]() ,
,![]() 直线
直线![]() 的解析式为
的解析式为![]() .
.
由![]() ,得
,得![]() ,
,![]() .
.![]() .
.
所以在该抛物线上不存在点![]() ,使得
,使得![]() 与
与![]() 相似.
相似.
解析:略

练习册系列答案
相关题目
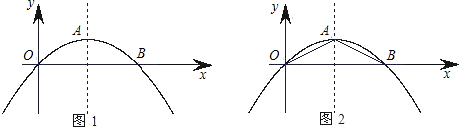

 轴上,CF交y轴于点B(0,2),且其面积为8.
轴上,CF交y轴于点B(0,2),且其面积为8.