题目内容
【题目】在平面直角坐标系
中，点
为
轴上的动点，点
为轴上方的动点，连接
，
，
．
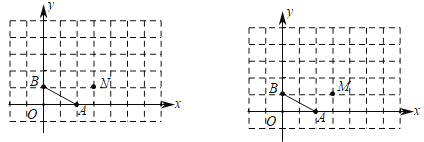
（1）如图1，当点在
轴上，且满足
的角平分线与
的角平分线交于点
，请直接写出
的度数；
（2）如图2，当点在轴上，的角平分线与的角平分线交于点，点
在
的延长线上，且满足
，求
；
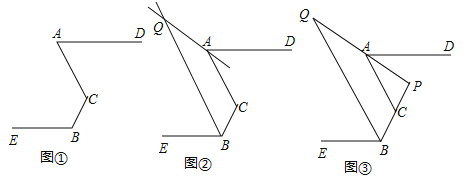
（3）如图3，当点在第一象限内，点
是
内一点，点
，
分别是线段，上一点，满足：
，
，
．
以下结论：①
；②
平分；③平分；④
．
正确的是：________．（请填写正确结论序号，并选择一个正确的结论证明，简写证明过程）．
【答案】（1）135°，（2）2；（3）②③④，理由见详解
【解析】
（1）根据三角形内角和定理（三角形的内角和是180°）和角平分线定理可求∠P的度数，进而得到答案；
（2）根据三角形外角的性质和角平分线定理可求解，进而可以得到答案；
（3）过点P作PF⊥OA于点F，过点P作PE⊥OB于点E，根据全等三角形的性质和角平分线性质，可求解．
解：(1) ∵∠AOB=90°，
∴∠OAB+∠OBA=90°，
∵AP平分∠OAB，BP平分∠OBA，
∴
，
∴
，
∴
；
(2) ∵BC平分∠ABO，
∴
，
∵
，
∴
，
∴
，
∴
；
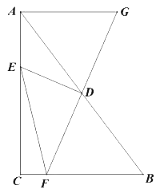
(3) 如图，连接OP，过点P作PF⊥OA于点F，过点P作PE⊥OB于点E，
∵∠ONP+∠OMP=180°，且∠OMP+∠PMF=180°，
∴∠PNO=∠PMF，且PN=PM，∠PEO=∠PFO=90°
∴△PEN≌△PMF（AAS）
∴PE=PF，且PE⊥OB，PF⊥OA
∴OP平分∠AOB，
如上图，作BH平分∠OBA，交OP延长线于点H，连接AH，
∵BH平分∠OBA，OH平分∠BOA，
∴AH平分∠OAB
∴
，
∴
，
∴
，
∴点H与点P重合，
∴AP平分∠OAB；BP平分∠OBA，
故②③正确，
∵PE=PF，OP=OP
∴Rt△OPE≌Rt△OPF（HL）
∴OE=OF，且OM＜OF=OE＜ON
故①错误
如上图，在AB上截取AQ=AM，
∵AM=AQ，∠OAP=∠BAP，AP=AP
∴△MAP≌△QAP（SAS），
∴∠PMA=∠PQA，
∴∠ONP=∠AQP，
∴∠BNP=∠BQP，且BP=BP，∠OBP=∠ABP，
∴△BPN≌△BPQ（AAS），
∴BN=BQ，
∴AB=AQ+BQ=AM+BN，
故④正确
故答案为：②③④．
