��Ŀ����
| |||||||||||||||||||
������
(1) |
�����⣺��AMN��ֱ�������� �����������OA=2��OM=4��ON=1����MN=OM+ON=4+1=5 ������Rt��AOM�У�AM= ������Rt��AON�У�AN= ������MN2=AM2+AN2 �������AMN��ֱ�������� |
(2) |
������(1)�еĽ��ۻ����� �����������OA=2��OM=��m��ON=n ������MN=OM+ON=n��m ������MN2=(n��m)2=n2��2mn+m2 ������mn=��4 ������MN2=n2��2��(��4)+m2=n2+m2+8 �����֡���Rt��AOM�У�AM= ������Rt��AON�У�AN= ������AM2+AN2=4+m2+4+n2=n2+m2+8 ������MN2=AM2+AN2 �������AMN��ֱ�������� |
(3) |
������mn=��4��n=4 ������ �����������ߵĽ���ʽΪy=a(x+1)(x�C4)�� �����������߾�����A(0��2)����C4a=2�����a=�C ���������������ߵĽ���ʽΪy=�C ������y=�C |
(4) |
���������ߵĶԳ�����x��Ľ���Q1���������� ������l��MN����ANM=��PNQ1����Rt��PNQ1��Rt��ANM �����������ߵĶԳ���Ϊx= ������NQ1=4�C ��������N��NQ2��AN���������ߵĶԳ����ڵ�Q2 ������Rt��PQ2N��Rt��NQ2Q1��Rt��PNQ1��Rt��ANM�������� ������ �����ߵ�Q2λ�ڵ������ޣ���Q2( ������ˣ����������ĵ����������ֱ���Q1( |

 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�





 �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ� 11����ͼ��ʾ����ֱ֪��a��b��c��d��e���ҡ�1=��2����3+��4=180�㣬��a��cƽ����Ϊʲô��
11����ͼ��ʾ����ֱ֪��a��b��c��d��e���ҡ�1=��2����3+��4=180�㣬��a��cƽ����Ϊʲô��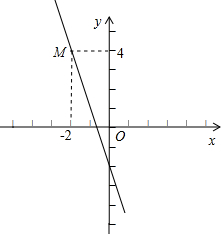 ��ͼ��ʾ����ֱ֪��y=kx-2����M�㣬���ֱ����x�ύ�������ֱ������������Χ�������ε������
��ͼ��ʾ����ֱ֪��y=kx-2����M�㣬���ֱ����x�ύ�������ֱ������������Χ�������ε������ ��ͼ��ʾ����ֱ֪��y=
��ͼ��ʾ����ֱ֪��y=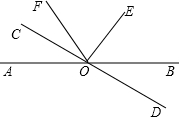 ��ͼ��ʾ����ֱ֪��AB��CD�ཻ�ڵ�O����COE=90�㣬OFƽ�֡�AOE������COF=26�㣬���BOD�Ķ�����
��ͼ��ʾ����ֱ֪��AB��CD�ཻ�ڵ�O����COE=90�㣬OFƽ�֡�AOE������COF=26�㣬���BOD�Ķ�����