题目内容
 如图,在△ABC中,∠BAC=45度,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,且EH=EB.小马虎在研究时得到四个结论:①∠ABC=45°;②AH=BC;③AE-BE=CH;④△AEC是等腰直角三角形.你认为正确的序号是
如图,在△ABC中,∠BAC=45度,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,且EH=EB.小马虎在研究时得到四个结论:①∠ABC=45°;②AH=BC;③AE-BE=CH;④△AEC是等腰直角三角形.你认为正确的序号是
- A.①②③④
- B.②③④
- C.①②③
- D.②③
B
分析:①根据AD⊥BC,若∠ABC=45°则∠BAD=45°,而∠BAC=45°,很明显不成立;
②③可以通过证明△AEH与△CEB全等得到;
④CE⊥AB,∠BAC=45°,所以是等腰直角三角形.
解答:①假设∠ABC=45°成立,
∵AD⊥BC,
∴∠BAD=45°,
又∠BAC=45°,
矛盾,所以∠ABC=45°不成立,故本选项错误;
∵CE⊥AB,∠BAC=45度,
∴AE=EC,
在△AEH和△CEB中,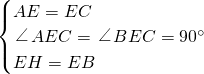 ,
,
∴△AEH≌△CEB(SAS),
∴AH=BC,故选项②正确;
又EC-EH=CH,
∴AE-EH=CH,故选项③正确.
∵AE=CE,CE⊥AB,所以△AEC是等腰直角三角形,故选项④正确.
∴②③④正确.
故选B.
点评:本题主要利用全等三角形的对应边相等进行证明,找出相等的对应边后,注意线段之间的和差关系.
分析:①根据AD⊥BC,若∠ABC=45°则∠BAD=45°,而∠BAC=45°,很明显不成立;
②③可以通过证明△AEH与△CEB全等得到;
④CE⊥AB,∠BAC=45°,所以是等腰直角三角形.
解答:①假设∠ABC=45°成立,
∵AD⊥BC,
∴∠BAD=45°,
又∠BAC=45°,
矛盾,所以∠ABC=45°不成立,故本选项错误;
∵CE⊥AB,∠BAC=45度,
∴AE=EC,
在△AEH和△CEB中,
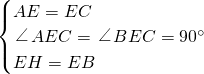 ,
,∴△AEH≌△CEB(SAS),
∴AH=BC,故选项②正确;
又EC-EH=CH,
∴AE-EH=CH,故选项③正确.
∵AE=CE,CE⊥AB,所以△AEC是等腰直角三角形,故选项④正确.
∴②③④正确.
故选B.
点评:本题主要利用全等三角形的对应边相等进行证明,找出相等的对应边后,注意线段之间的和差关系.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 20、如图,在△ABC中,∠BAC=45°,现将△ABC绕点A逆时针旋转30°至△ADE的位置,使AC⊥DE,则∠B=
20、如图,在△ABC中,∠BAC=45°,现将△ABC绕点A逆时针旋转30°至△ADE的位置,使AC⊥DE,则∠B= 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为 2、如图,在△ABC中,DE∥BC,那么图中与∠1相等的角是( )
2、如图,在△ABC中,DE∥BC,那么图中与∠1相等的角是( ) 如图,在△ABC中,AB=AC,且∠A=100°,∠B=
如图,在△ABC中,AB=AC,且∠A=100°,∠B=