题目内容
 如图所示,四边形ABCD由四个直角三角形拼凑而成,它们的公共直角顶点为O.已知△AOB,△BOC,△COD的面积分别是20,10,16,那么△AOD的面积是
如图所示,四边形ABCD由四个直角三角形拼凑而成,它们的公共直角顶点为O.已知△AOB,△BOC,△COD的面积分别是20,10,16,那么△AOD的面积是
- A.20
- B.26
- C.32
- D.48
C
分析:根据直角三角形的面积等于两直角边乘积的一半列式表示出△AOB,△BOC,△COD,然后整理求出AO•OD的值,从而求出△AOD的面积.
解答:根据题意得,S△AOB= ×AO•BO=20①,
×AO•BO=20①,
S△BOC= ×BO•CO=10②,
×BO•CO=10②,
S△COD= ×DO•CO=16③,
×DO•CO=16③,
①÷②得 =2,
=2,
由③得 =
= ,
,
∴AO•DO=64,
∴S△AOD= ×AO•DO=32.
×AO•DO=32.
故选C.
点评:本题考查了三角形的面积计算,直角三角形的面积等于两直角边乘积的一半,本题难点在于利用边的关系的转化得到AD•DO的值.
分析:根据直角三角形的面积等于两直角边乘积的一半列式表示出△AOB,△BOC,△COD,然后整理求出AO•OD的值,从而求出△AOD的面积.
解答:根据题意得,S△AOB=
 ×AO•BO=20①,
×AO•BO=20①,S△BOC=
 ×BO•CO=10②,
×BO•CO=10②,S△COD=
 ×DO•CO=16③,
×DO•CO=16③,①÷②得
 =2,
=2,由③得
 =
= ,
,∴AO•DO=64,
∴S△AOD=
 ×AO•DO=32.
×AO•DO=32.故选C.
点评:本题考查了三角形的面积计算,直角三角形的面积等于两直角边乘积的一半,本题难点在于利用边的关系的转化得到AD•DO的值.

练习册系列答案
相关题目
 21、如图所示,四边形ABCD是平行四边形,E,F分别在AD,CB的延长线上,且DE=BF,连接FE分别交AB,CD于点H,G.
21、如图所示,四边形ABCD是平行四边形,E,F分别在AD,CB的延长线上,且DE=BF,连接FE分别交AB,CD于点H,G. 12、如图所示,四边形ABCD为⊙O的内接四边形,E为AB延长线的上一点,∠CBE=40°,则∠AOC等于( )
12、如图所示,四边形ABCD为⊙O的内接四边形,E为AB延长线的上一点,∠CBE=40°,则∠AOC等于( )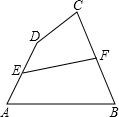 如图所示,四边形ABCD中,E、F分别为AD、BC的中点.
如图所示,四边形ABCD中,E、F分别为AD、BC的中点.
