题目内容
如图1，在边长为a的正方形纸片的4个角都剪去1个长和宽分别是x、y的长方形．（1）试用a、x、y表示纸片剩余部分的面积，并指出其二次项系数的和是多少？
（2）如图2，在边长为a的正方形纸片的4个角都剪去1个相同的扇形，扇形的半径为r，用r、a表示纸片剩余部分的面积为
a2-πr2
a2-πr2
，剩余部分图形的周长为4a-8r+2πr
4a-8r+2πr
．分析：（1）根据剩余部分的面积等于正方形的面积减去四个长方形的面积列式整理即可得解；
（2）根据剩余部分的面积等于正方形的面积减去四个扇形的面积列式整理即可；周长等于四段剩余的边长加上四个扇形的弧长（即一个圆的周长）．
（2）根据剩余部分的面积等于正方形的面积减去四个扇形的面积列式整理即可；周长等于四段剩余的边长加上四个扇形的弧长（即一个圆的周长）．
解答：解：（1）纸片剩余部分的面积=a2-4xy，
二次项系数的和为：1+（-4）=-3；
（2）纸片剩余部分的面积=a2-πr2，
剩余部分图形的周长为=4（a-2r）+2πr=4a-8r+2πr．
故答案为：a2-πr2；4a-8r+2πr．
二次项系数的和为：1+（-4）=-3；
（2）纸片剩余部分的面积=a2-πr2，
剩余部分图形的周长为=4（a-2r）+2πr=4a-8r+2πr．
故答案为：a2-πr2；4a-8r+2πr．
点评：本题考查了列代数式，观察图形得到剩余部分的面积和周长的表示方法是解题的关键．
练习册系列答案
相关题目
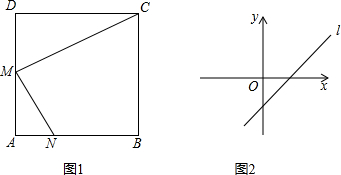
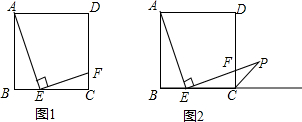
如图1，在边长为a的正方形中剪去一个边长为b的小正形（a＞b），把剩下部分拼成一个梯形（如图2），利用这两幅图形面积，可以验证的乘法公式是