Question

【题目】如图，在平面直角坐标系中，已知A（0，5）， B（a，b），且a，b满足b＝＋－1．

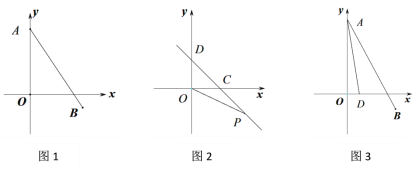
(1)如图，求线段AB的长；

(2)如图，直线CD与x轴、y轴正半轴分别交于点C，D，∠OCD＝45°，第四象限的点P（m，n）在直线CD上，且mn＝－6，求OP2－OC2的值；

(3)如图，若点D（1，0），求∠DAO ＋∠BAO的度数.

Answer 1

【答案】(1) ;(2)12 ;(3)45°

【解析】

（1）根据b＝＋－1可求得a、b的值，得到B点的坐标，根据两点间坐标公式即可求解.

（2）根据直线CD与x轴、y轴正半轴分别交于点C，D，∠OCD＝45°，可知直线CD平行于y= -x，可设直线CD解析式为y= -x +b，代入P点坐标，得到m、n、b的关系，代入计算即可.

(3)取点D关于y轴的对称点，运用两点间坐标公式及勾股定理逆定理可判断△AB是等腰直角三角形，即可求得∠BA的值，等量代换即可.

(1)∵b＝＋－1

∴a=4 ,b= -1

∴B点坐标为：（4，-1）

∵A（0，5）

∴AB=)

（2）∵直线CD与x轴、y轴正半轴分别交于点C，D，∠OCD＝45°

∴直线CD平行于y= -x

设直线CD解析式为y= -x +b

则B点坐标为（b，0）

把点P（m，n）代入得：n= -m +b

∴b= m+n

∴OP2－OC2=

∵mn＝－6

∴OP2－OC2

（3）取点D关于y轴的对称点，则∠DAO=∠，

∴∠DAO ＋∠BAO=∠＋∠BAO=∠BA

∵点D（1，0）

∴（-1，0）

由（1）得：A（0，5），B（4，-1）

∴A=，，

∴A ，

∴△A是等腰直角三角形

∴∠DAO ＋∠BAO=∠BA=45°