题目内容
直角三角形的两直角边分别为15和20，则斜边上的高为
- A.9
- B.10
- C.11
- D.12
D
分析：根据勾股定理求得斜边的长，再根据三角形的面积公式即可求得高的长．
解答：根据勾股定理求出斜边的长为
=25，
设斜边上的高为x，根据面积相等列方程得
×15×20=×25x，解得x=12，
故选D．
点评：根据面积相等列方程解答，是求直角三角形斜边上的高常用的方法．
分析：根据勾股定理求得斜边的长，再根据三角形的面积公式即可求得高的长．
解答：根据勾股定理求出斜边的长为
=25，设斜边上的高为x，根据面积相等列方程得
×15×20=×25x，解得x=12，故选D．
点评：根据面积相等列方程解答，是求直角三角形斜边上的高常用的方法．
练习册系列答案
相关题目
，
表示直角三角形的两直角边（
），下列四个说法：
，②
，③
，④
.
，
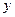表示直角三角形的两直角边（
），下列四个说法：①
，②
，③
，④
.其中说法正确的是 ……………………【 】
，
表示直角三角形的两直角边（
），下列四个说法：
，②
，③
，④
.