题目内容
如图，已知AB∥CE，DB平分∠ADC，AE∥BD，∠C=2∠E，求证：四边形ABCD是等腰梯形．分析：先根据AE∥BD得出∠E=∠BDC，再根据DB平分∠ADC得出∠ADC=2∠E，由于∠C=2∠E，所以∠ADC=∠C，再根据AB∥CE即可得出结论．
解答：解：∵AE∥BD，
∴∠E=∠BDC，
∵DB平分∠ADC，
∴∠ADC=2∠E，
∵∠C=2∠E，
∴∠ADC=∠C，
∵AB∥CE，
∴四边形ABCD是等腰梯形．
∴∠E=∠BDC，
∵DB平分∠ADC，
∴∠ADC=2∠E，
∵∠C=2∠E，
∴∠ADC=∠C，
∵AB∥CE，
∴四边形ABCD是等腰梯形．
点评：本题考查的是等腰梯形的判定，熟知两腰相等的梯形叫做等腰梯形是解答此题的关键．
练习册系列答案
相关题目
8、如图，已知AB∥CE，∠C=30°，BC平分∠ABD，则∠BDC=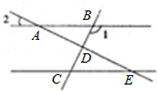
如图，已知AB∥CE，AE与BC交于点D，∠1=120°，∠2=30°，则下列说法不正确的（ ）
如图，已知AB∥CE，∠A=∠E，试说明：∠CGD=∠FHB．