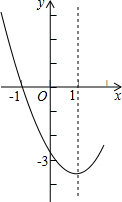题目内容
如图,平面直角坐标系中有一矩形纸片OABC,O为原点,点A,C分别在x轴,y轴上,点B坐标为(m,
)(其中m>0),在BC边上选取适当的点E和点F,将△OCE沿OE翻折,得到△OGE;再将△ABF沿AF翻折,恰好使点B与点G重合,得到△AGF,且∠OGA=90度.
 (1)求m的值;
(1)求m的值;
(2)求过点O,G,A的抛物线的解析式和对称轴;
(3)在抛物线的对称轴上是否存在点P,使得△OPG是等腰三角形?若不存在,请说明理由;若存在,直接答出所有满足条件的点P的坐标(不要求写出求解过程).
| 2 |
 (1)求m的值;
(1)求m的值;(2)求过点O,G,A的抛物线的解析式和对称轴;
(3)在抛物线的对称轴上是否存在点P,使得△OPG是等腰三角形?若不存在,请说明理由;若存在,直接答出所有满足条件的点P的坐标(不要求写出求解过程).
(1)解法一:∵B(m,
),
由题意可知AG=AB=
,OG=OC=
,OA=m(2分)
∵∠OGA=90°,
∴OG2+AG2=OA2
∴2+2=m2.
又∵m>0,
∴m=2.
解法二:∵B(m,
),
由题意可知AG=AB=
,OG=OC=
,OA=m
∵∠OGA=90°,
∴∠GOA=∠GAO=45°
∴m=OA=
=
=2.
(2)解法一:过G作直线GH⊥x轴于H,
 则OH=1,HG=1,故G(1,1).
则OH=1,HG=1,故G(1,1).
又由(1)知A(2,0),
设过O,G,A三点的抛物线解析式为y=ax2+bx+c
∵抛物线过原点,
∴c=0.
又∵抛物线过G,A两点,
∴
,
解得
,
∴所求抛物线为y=-x2+2x,
它的对称轴为x=1.
解法二:过G作直线GH⊥x轴于H,
则OH=1,HG=1,故G(1,1).
又由(1)知A(2,0),
∴点A,O关于直线l对称,
∴点G为抛物线的顶点.
于是可设过O,G,A三点的抛物线解析式为y=a(x-1)2+1,
∵抛物线过点O(0,0),
∴0=a(0-1)2+1,
解得a=-1,
∴所求抛物线为y=(-1)(x-1)2+1=-x2+2x
它的对称轴为x=1.
(3)答:存在
满足条件的点P有(1,0),(1,-1),(1,1-
),(1,1+
).
| 2 |
由题意可知AG=AB=
| 2 |
| 2 |
∵∠OGA=90°,
∴OG2+AG2=OA2
∴2+2=m2.
又∵m>0,
∴m=2.
解法二:∵B(m,
| 2 |
由题意可知AG=AB=
| 2 |
| 2 |
∵∠OGA=90°,
∴∠GOA=∠GAO=45°
∴m=OA=
| OG |
| cos∠GOA |
| ||
| cos45° |
(2)解法一:过G作直线GH⊥x轴于H,
 则OH=1,HG=1,故G(1,1).
则OH=1,HG=1,故G(1,1).又由(1)知A(2,0),
设过O,G,A三点的抛物线解析式为y=ax2+bx+c
∵抛物线过原点,
∴c=0.
又∵抛物线过G,A两点,
∴
|
解得
|
∴所求抛物线为y=-x2+2x,
它的对称轴为x=1.
解法二:过G作直线GH⊥x轴于H,
则OH=1,HG=1,故G(1,1).
又由(1)知A(2,0),
∴点A,O关于直线l对称,
∴点G为抛物线的顶点.
于是可设过O,G,A三点的抛物线解析式为y=a(x-1)2+1,
∵抛物线过点O(0,0),
∴0=a(0-1)2+1,
解得a=-1,
∴所求抛物线为y=(-1)(x-1)2+1=-x2+2x
它的对称轴为x=1.
(3)答:存在
满足条件的点P有(1,0),(1,-1),(1,1-
| 2 |
| 2 |

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目

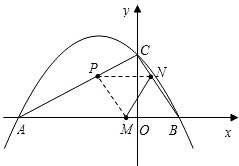 BC,B、C两点的坐标分别为B(1,0)、
BC,B、C两点的坐标分别为B(1,0)、