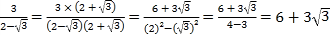题目内容
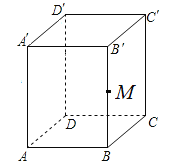
【题目】如图，长方体ABCD-A'B'C'D'是个无上底长方体容器，长AB＝5cm，宽BC＝3cm，高AA′＝8cm，甜食点M在容器内侧，位于侧棱BB′的中点，一只蚂蚁从容器外部的A爬到点M处吃甜食，这只蚂蚁爬行的最短路径是（ ）cm
A.
B.13C.
D.14
【答案】B
【解析】
做点A关于A′B′的对称点E，连接ME交A′B′于点F，连接AF，则AF+MF即为蚂蚁的最短路线，然后结合矩形和对称的性质，利用勾股定理列方程求解．
解：做点A关于A′B′的对称点E，连接ME交A′B′于点F，连接AF，则AF+MF即为蚂蚁的最短路线
又由对称的性质可知，A′F垂直平分AE
∴AF=EF
∴蚂蚁的最短路线为EF+MF，即ME的长度
过点M做MN⊥AA′，
由题意可知：AE=2AA′=16，MN=AB=5，AN=BM= 
AA′=4
∴NE=16-4=12
在Rt△MNE中，
故选：B．
练习册系列答案
相关题目
【题目】我们约定：如果身高在选定标准的±2%范围之内都称为“普启遍身高”．为了了解某校九年级男生中具有“普遍身高”的人数，我们从该校九年级男生中随机抽出10名男生，分别测量出他们的身高(单位：cm)，收集并整理如下统计表：
男生 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
身高x(cm) | 163 | 171 | 173 | 159 | 161 | 174 | 164 | 166 | 169 | 164 |
根据以上信息，解答如下问题：
(1)计算这组数据的三个统计量：平均数、中位数、众数；
(2)请你选择其中一个统计量作为选定标准，找出这10名男生中具有“普遍身高”是哪几位男生？并说明理由．
