题目内容
 如图所示,梯形ABCD关于y轴对称,点A的坐标为(-3,3),点B的坐标为(-2,0).
如图所示,梯形ABCD关于y轴对称,点A的坐标为(-3,3),点B的坐标为(-2,0).(1)写出点C和点D的坐标;
(2)求出梯形ABCD的面积.
分析:(1)点C和点B关于y轴对称,点D和点A关于y轴对称,继而即可写出答案;
(2)求出OE的长,然后根据梯形的面积公式求解即可.
(2)求出OE的长,然后根据梯形的面积公式求解即可.
解答:解:(1)∵点A的坐标为(-3,3),点B的坐标为(-2,0),
又点C和点B关于y轴对称,点D和点A关于y轴对称,
∴点C和点D的坐标分别为:(2,0),(3,3);
(2)S梯形ABCD=
(AD+BC)•OE
=
×(4+6)×3=15.
又点C和点B关于y轴对称,点D和点A关于y轴对称,
∴点C和点D的坐标分别为:(2,0),(3,3);
(2)S梯形ABCD=
| 1 |
| 2 |
=
| 1 |
| 2 |
点评:本题考查轴对称的性质,难度适中,解题关键是熟练掌握并熟记梯形的面积公式.

练习册系列答案
相关题目
 如图所示,在△ABC中,AB=AC,BD,CE分别为∠ABC,∠ACB的平分线.
如图所示,在△ABC中,AB=AC,BD,CE分别为∠ABC,∠ACB的平分线. 已知:如图所示,梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=BC=4
已知:如图所示,梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=BC=4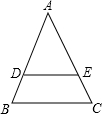 如图所示,在△ABC中,DE∥BC,△ADE和梯形DBCE的面积相等,则AD:DB=
如图所示,在△ABC中,DE∥BC,△ADE和梯形DBCE的面积相等,则AD:DB=
 梯形的边运动,设点P运动的路程为x,△ABP的面积为y,函数图象如图②所示,则△ABC面积为
梯形的边运动,设点P运动的路程为x,△ABP的面积为y,函数图象如图②所示,则△ABC面积为