题目内容
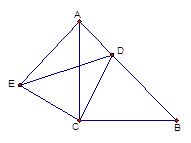
已知:如图,△ABC和△ECD都是等腰直角三角形,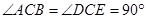 ,D为AB边上一点,
,D为AB边上一点,
求证:(1)△ACE≌△BCD;(2)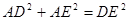
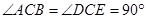 ,D为AB边上一点,
,D为AB边上一点,求证:(1)△ACE≌△BCD;(2)
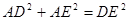

(1) ∵ 
∴
即 …………2分
…………2分
∵
∴ △BCD≌△ACE …………4分
(2)∵ ,
,
∴ …………5分
…………5分
∵ △BCD≌△ACE
∴
∴
∴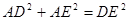

∴

即
 …………2分
…………2分∵

∴ △BCD≌△ACE …………4分
(2)∵
 ,
,∴
 …………5分
…………5分∵ △BCD≌△ACE
∴

∴

∴
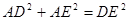
(1)本题要判定△ACE≌△BCD,已知△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,则DC=EA,AC=BC,∠ACB=∠ECD,又因为两角有一个公共的角∠ACD,所以∠BCD=∠ACE,根据SAS得出△ACE≌△BCD.
(2)由(1)的论证结果得出∠DAE=90°,AE=DB,从而求出AD2+DB2=DE2.
(2)由(1)的论证结果得出∠DAE=90°,AE=DB,从而求出AD2+DB2=DE2.

练习册系列答案
相关题目
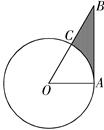
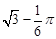
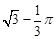
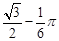
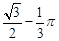
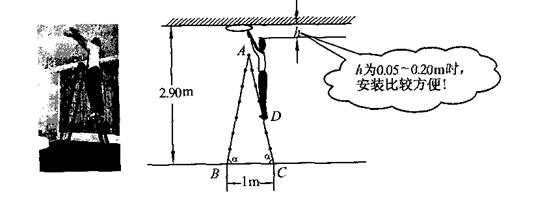
 角.在A处测得树顶D的俯角为15
角.在A处测得树顶D的俯角为15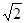 ≈1.4
≈1.4 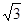 ≈1.7)
≈1.7)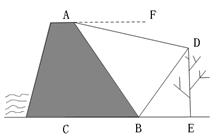
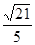
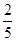


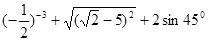
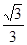 ,则cosB=_______;
,则cosB=_______;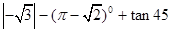 º
º