题目内容
 图中的小方格都是边长为1的正方形,四边形ABCD的顶点O点都在正方形的顶点上.
图中的小方格都是边长为1的正方形,四边形ABCD的顶点O点都在正方形的顶点上.(1)以点O为中心,在如图的方格纸内将四边形ABCD放大到原来的2倍,得到四边形A′B′C′D′,画出放大后的图形A′B′C′D′.
(2)四边形A′B′C′D′绕点A′顺时针旋转90°,画出旋转得到的四边形A″B″C″D″,并求边A′D′在旋转过程中扫过的图形面积.
分析:(1)根据以点O为中心,将四边形ABCD放大到原来的2倍,即延长AB,DC找出对应点即可得出;
(2)根据图象旋转的性质得出,再利用扇形面积求法得出答案.
(2)根据图象旋转的性质得出,再利用扇形面积求法得出答案.
解答: 解:(1)如图所示;
解:(1)如图所示;
(2)如图所示;
边A′D′在旋转过程中扫过的图形面积为:
=16π.
 解:(1)如图所示;
解:(1)如图所示;(2)如图所示;
边A′D′在旋转过程中扫过的图形面积为:
| 90π×64 |
| 360 |
点评:此题主要考查了扇形的面积公式以及图象的旋转等知识,根据图象旋转前后大小不变得出是解题关键.

练习册系列答案
相关题目
 18、如图,图中的小方格都是边长为1的正方形,△ABC与△A/B/C/是关于点0为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
18、如图,图中的小方格都是边长为1的正方形,△ABC与△A/B/C/是关于点0为位似中心的位似图形,它们的顶点都在小正方形的顶点上. 21、如图,图中的小方格都是边长为1的正方形,点E、A、B、C都在小正方形的顶点上.
21、如图,图中的小方格都是边长为1的正方形,点E、A、B、C都在小正方形的顶点上. 21、如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标为A (0,-2)、B (3,-1)、C (2,1).
21、如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标为A (0,-2)、B (3,-1)、C (2,1).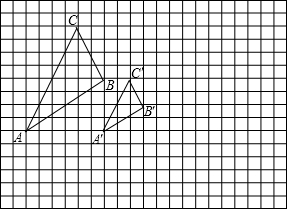 们的顶点都在小正方形的顶点上.
们的顶点都在小正方形的顶点上. 如图图中的小方格都是边长为1的正方形,△ABC的顶点都在小正方形的顶点上,请完成以下题目
如图图中的小方格都是边长为1的正方形,△ABC的顶点都在小正方形的顶点上,请完成以下题目