题目内容
 已知:如图,四边形ABCD中AC、BD相于点O,AB=AC,AB⊥AC,BD平分∠ABC且BD⊥CD,OE⊥BC于E,OA=1.
已知:如图,四边形ABCD中AC、BD相于点O,AB=AC,AB⊥AC,BD平分∠ABC且BD⊥CD,OE⊥BC于E,OA=1.(1)求OC的长;
(2)求证:BO=2CD.
分析:(1)由于BD平分∠ABC且BD⊥CD,OE⊥BC,可知O为∠ABC平分线上的一点,根据角平分线上的点到角的两边的距离相等,求出OE的长,由于△ABC为等腰直角三角形,故知∠BCA=45°,∠CBA=45°,可知△OEC为等腰直角三角形,利用勾股定理可求出OC的长;
(2)在直角三角形ABO中,由于AB=AC=1+
,AO=1,利用勾股定理求出BO的长,易得,△AOB∽△DOC,
利用相似三角形的性质求出CD的长,即可得出BO=2CD.
(2)在直角三角形ABO中,由于AB=AC=1+
| 2 |
利用相似三角形的性质求出CD的长,即可得出BO=2CD.
解答:解:(1)∵BD平分∠ABC且BD⊥CD,OE⊥BC,
∴OE=OA=1,
∵△ABC为等腰直角三角形,
∴∠BCA=45°,
∵OE⊥BC,
∴△OEC为等腰直角三角形,
∴OC=
=
;
证明:(2)Rt△ABO中,AB=AC=1+
,AO=1,
BO=
=
,
易得,△AOB∽△DOC,
=
,
即
=
,
CD=
=
,
则2CD=
,
可得BO=2CD.
∴OE=OA=1,
∵△ABC为等腰直角三角形,
∴∠BCA=45°,
∵OE⊥BC,
∴△OEC为等腰直角三角形,
∴OC=
| 12+12 |
| 2 |
证明:(2)Rt△ABO中,AB=AC=1+
| 2 |
BO=
(1+
|
4+2
|
易得,△AOB∽△DOC,
| OB |
| OC |
| AB |
| CD |
即
| ||||
|
1+
| ||
| CD |
CD=
|
| ||||
| 2 |
则2CD=
4+2
|
可得BO=2CD.
点评:本题考查了等腰三角形的性质、勾股定理、角平分线的性质、相似三角形的判定与性质,综合性较强,要注意计算过程中无理数的相关计算法则.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
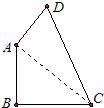 已知,如图,四边形ABCD中∠B=90°,AB=9,BC=12,AD=8,CD=17.
已知,如图,四边形ABCD中∠B=90°,AB=9,BC=12,AD=8,CD=17.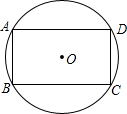 已知:如图,四边形ABCD内接于⊙O,且AB∥CD,AD∥BC,
已知:如图,四边形ABCD内接于⊙O,且AB∥CD,AD∥BC, 已知,如图,四边形ABCD是正方形,E、F分别是AB和AD延长线上的点,且BE=DF
已知,如图,四边形ABCD是正方形,E、F分别是AB和AD延长线上的点,且BE=DF 已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少?
已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少? 已知:如图,四边形ABCD及一点P.
已知:如图,四边形ABCD及一点P.