题目内容
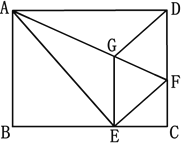
【题目】如图,将矩形ABCD沿线段AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:△AGE≌△AGD
(2)探究线段EG、GF、AF之间的数量关系,并说明理由;
(3)若AG=6,EG=2![]() ,求BE的长.
,求BE的长.
【答案】(1)证明见解析;
(2)AF·GF=2EG![]() ,证明见解析;
,证明见解析;
(3)BE的长为![]() .
.
【解析】(1)证明:∵△AEF是由△ADF折叠得到的
∴AD=AE,∠DAG=∠EAG
又∵AG=AG
∴△AGE≌△AGD
(2)AF×GF=2EG![]() 证明如下:
证明如下:
连接DE交GF于点O

∵△AEF是由△ADF折叠得到的
∠DAG=∠EAG,DF=EF
∵△AGE≌△AGD
∴GD=GE,∠ AGD=∠AGE
∴∠ FGD=∠FGE
∵EG∥CD
∴∠DFG=∠FGE
∴∠ FGD=∠DFG
∴GD=DF
∴GD=EG=EF=DF
∴四边形DGEF是菱形
AF⊥DE,OF=![]() GF
GF
∴∠ADF=∠DOF =90°
又∵∠DFO=∠DFA
∴△DFO∽△AFD
∴![]()
∴OF×AF=DF![]()
∵OF=![]() GF, DF=EG
GF, DF=EG
∴![]() GF×AF= EG
GF×AF= EG![]()
即:AF×GF=2EG![]()
(2)过点G作GH⊥CD于H

则四边形CHGE是矩形,
∴CE=GH
设GF=x,则AF=6+x
∵AF×GF=2EG![]() EG=2
EG=2![]()
∴x(6+x)=40
解得:x=4
∴GF=4,
∴ AF=6+4=10
在Rt△AEF中
AE=![]()
∴BC=AD=AE=4![]()
∵GH∥AD
∴△FGH∽△FAD
∴![]()
∴![]()
∴CE=GH=![]()
∴BE=BC-CE=4![]() -
-![]() =
=![]()

练习册系列答案
相关题目