Question

【题目】如图，已知为坐标原点，点的坐标为，的半径为，过作直线平行于轴，设与轴交点为，点在上运动．

（1）当点运动到圆上时，求此时点的坐标

（2）如图，当点的坐标为时，连接，作于，求的长和的长

（3）在（2）条件下，试判断直线与的位置关系，并说明理由．

Answer 1

【答案】（1）当点运动到点时坐标为，当点运动到点时坐标为（3），；（2）直线与相离，理由详见解析.

【解析】

（1）当点在上运动时，点的纵坐标与点的纵坐标相同，根据圆的半径的长度即可得到答案；

（2）在中，利用勾股定理即可求得OP的长，再根据相似三角形的判定与性质即可求得AM的长；

（3）根据（2）中AM的长即可判断.

解：（1）如图，∵直线平行于轴，

∴当点在上运动时，点的纵坐标与点的纵坐标相同，

当点运动到点时坐标为，

当点运动到点时坐标为；

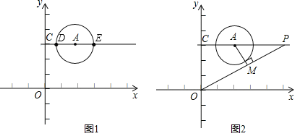
（2）∵，

∴，，

在中，，

∵，，

∴，

∴，

∴

∴；

（3）∵，即，

∴直线与相离．