题目内容
如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F.

(1)当PE⊥AB,PF⊥BC时,如图1,则 的值为 ;
的值为 ;
(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求 的值;
的值;
见解析
【解析】
试题分析:(1)当PE⊥AB,PF⊥BC时,四边形PEBF是矩形,所以PF=BE,因为在矩形ABCD中,点P是AC的中点,所以AE=BE=PF,又∠APE=∠ACB=30°,可得PE= AE,所以
AE,所以 ;(2)过点P作PM⊥AB于点M,PN⊥BC于点N,可证△PME∽△PNF.然后可得
;(2)过点P作PM⊥AB于点M,PN⊥BC于点N,可证△PME∽△PNF.然后可得 .
.
试题解析:(1) .
.
(2)如答图1,

过点P作PM⊥AB于点M,PN⊥BC于点N,则PM⊥PN.
∵PM⊥PN,PE⊥PF,∴∠EPM=∠FPN.
又∵∠PME=∠PNF=90°,∴△PME∽△PNF.
∴ .
.
由(1)知, ,
,
∴ .
.
考点:1.矩形的性质;2.解直角三角形;3.相似三角形的判定与性质.

练习册系列答案
相关题目
(本题满分8分)某公司欲招聘业务员一名,现对A、B、C三名候选人分别进行笔试、面试测试,成绩如下表:
测试项目 | 测试成绩(分) | ||
甲 | 乙 | 丙 | |
笔试 | 75 | 85 | 90 |
面试 | 93 | 75 | 72 |
(1)如果按照三人测试成绩的平均成绩录取人选,那么谁将被录用?
(2)根据实际需要,公司想将丙录用,请兼顾笔试、面试两个方面,你确定的方案是什么?写出理由.
 ,AB=10,则AC的长为
,AB=10,则AC的长为 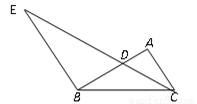
 =0,则锐角θ的大小是 .
=0,则锐角θ的大小是 . = .
= .
 .
.